The LCAO method

Linear Combination of Atomic Orbitals (LCAO)

Due to the double slit experiment, we are already familiar with one fundamental principle of quantum mechanics, i.e. that the true probability amplitude for a system can be described as a linear combination of more fundamental single amplitudes. Now we try to determine molecular energy levels and wave functions. Therefore, we need to solve the Schroedinger equation Hψ_n = E_n ψ_n, with the molecule's Hamiltonian operator H and ψ_n as a representation of the molecular orbitals. For analyzing the system, we expand the eigenfunction ψ_n by employing well known fundamental functions φ_k. It is understood that these functions φ_k are no eigenfunctions with respect to Hψ_n: y = ∑_k c_kφ_k (to simplify, index n has been omitted here). The following explanations treat the problem in an abstract mathematical manner. Anyone who wishes getting a first impression of the principles is invited to click here.

The most conspicious and - when compared with atomic orbitals - distinctive property is that molecular orbitals are polycentric. The best way of describing an electron is to state that it moves within an orbital that is located around both (respectively all) nuclei of the molecule's atoms. Now we want to describe molecular orbitals ψ as a linear combination of atomic orbitals φ (LCAO = Linear Combination of AtomicOrbitals). The appropriate φ is soon to be presented. In a general treatment, first we expand the function ψ for any molecule using functions φ and use the common abbreviations. The equations in the left column refer to the general case where the number of functions φ remains open, whereas the equations in the right column refer to diatomic molecules for which two functions φ are employed.

Hψ = E ψ
ψ = ∑_k c_kφ_k	ψ = c_Aφ_A + c_Bφ_B
H∑_k c_kφ_k = E ∑_k c_k&phi,_k	H(c_Aφ_A+c_Bφ_B) = E(c_Aφ_A+c_Bφ_B)
Multiplication with φ_i* and ∫:	Multiplication with φ_A* and ∫:
∑_k c_k∫φ_i* Hφ_kdτ = E ∑_kc_k∫φ_i·φ_kdτ	c_A∫φ_A* Hφ_A + c_B ∫φ_AHφ_B = Ec_A + Ec_B· ∫φ_Aφ_B
H_ik = ∫φ_i* Hφ_kdτ S_ik = ∫φ_i*φ_kdτ	H_AA= ∫φ_A* Hφ_A; H_AB= ∫φ_A* Hφ_B; S_AB = ∫φ_A*φ_B
∑_k c_k (H_ik−E·S_ik) = 0	c_A(H_AA−E) + c_B(H_AB − E·S_AB) = 0 c_A(H_BA − E·S_BA) + c_B (H_BB−E) = 0

We recieved a linear system of equations, the so-called "secular equations". Besides the trivial case with c_k = 0, there is only one solution where the secular determinant disappears. For the diatomic molecule, the problem is easily solved by transforming both equations to have c_A/c_B on the left side and equate both equations of the system. Maybe it is confusing to obtain the term ∫φ_i*φ_kdτ as we have learned that the functions, i.e. the atomic orbitals, are orthogonal. This still holds true, but in contrast to AOs of single atoms, in our case, each AO has a centre of its own because there is a shift in position. In consequence, they are not necessarily orthogonal.
We already anticipate that it would be desirable to know the case where the integral ∫ φ_A*φ_Bdτ disappears. Anyone who wants to consider the problem for himself in advance may combine an atomic orbital of atom A, e.g. 1s_A with atomic orbitals like 2p_x, 2p_y or 2p_z of atom B and pay attention to the case where the integral becomes zero. But be aware that H_AA, H_AB, S_AB etc. appear in all applications of the LCAO-MO-theory and thus it is indispensible to know their physical meaning. Often, you will find another representation:

α_A = H_AA = ∫φ_A* Hφ_Adτ
α_B = H_BB = ∫φ_B* Hφ_Bdτ
β = H_AB = H_BA = ∫φ_A* Hφ_Bdτ S_BA = S_AB = S = ∫φ_A*φ_Bdτ

Using this notation, the equations for the AB-system become:

c_A(α_A−E) + c_B(β−E·S) = 0
c_A(β−E·S) + c_B(α_B−E) = 0

First, let's focus on the meaning of involved quantities: Under the assumption of a normalized function φ_A the α_A represents roughly the energy of an electron imagined to move in orbital φ_A of atom A; an analogous interpretation applies to α_B. Energy α_A is below E_A for the wave function φ_A of an electron bound solely to nucleus A because in H, there is also a component that represents attraction to nucleus B. α_A is the expected value for the energy that is described by φ_A. Especially the sphere close to nucleus A contributes to α_A where φ_A is large too, and this is as well the sphere where H resembles the operator of the unbound atom. Thus α_A (oder α_B) is approximately the energy of an electron in φ_A (or φ_B) close to nucleus A (or B) which is slightly changed by the presence of the other atom. As α_A and α_B contain terms for Coulomb's forces, they are called the coulombic integral. For a certain type of orbital, the absolute value of α increases from the left to the right for the elements of one row in the periodic table of elements. Note that the same increase is found for the atom's electronegativity or "attraction" towards electrons.

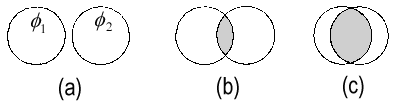The overlap S₁₂ between two identical s-orbitals φ₁ and φ₂:
(a) S₁₂ ≈ 0; (b) small S₁₂; (c) S₁₂ →1.

The integrals above depend both on φ_A and φ_B. Obviously, the values for β and S are strongly dependent on possible overlap between the two atomic orbitals. S is called the overlap integral and β resonance integral . The solution of the secular equations for homonuclear molecules (consisting identical atoms A and B) with α_A = α_B differs from that for heteronuclear molecules (α_A ≠α_B). Thus, we treat the two cases independently. To comprehend the essence, we first focus on the most simple molecule - the H₂⁺-Ion. Maybe, the laboratory chemist is disappointed now as he never faces this ion. But even he won't be able to treat complicated molecules without an understanding for the basic ones.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.