Homonuclear Molecules A₂

For two atomic homonuclear molecules like H₂, O₂, N₂ etc, the LCAO expansion represents an especially simple approach. The progress made with the ionic molecule H₂⁺ is as well valuable for other homonuclear species. We will treat theses molecules in the same way. Of course, we will face some additional points, especially for bonds established by more than one electron. Analogous to atomic orbitals, we introduce molecular orbitals of different energy. The molecule's electrons are distributed among them in a way that the orbitals with the lowest energies are occupied first and the Pauli principle is accomplished. For a first approximation, we regard these orbitals as linear combinations of atomic orbitals. Taking the two 1s orbitals of the hydrogen atom, we obtain the two MOs that already appeared in the previous chapter that dealt with H₂⁺:

In order to have a concise presentation, the various coeffients for normalization are omitted in both equations. Moreover, greec minuscules σ (analogous to s for the atoms) are introduced to represent the MOs. A consideration of the indices follows below. Note that α_A and α_B in the secular equations are identical for homonuclear molecules: α_A = α_B = α. Therefore, both wave functions are introduced with the same weight but maybe with opposite signs.

Thus, in cases where the overlap integral S is, compared with 1, small, an originally degenerated pair of energy values α splits symmetrically into two values above and below the original energy level. The level of reduced energy is called the bonding MO as it is below the energy level of the separated atoms. The level of increased energy is above the energy level of the separated atoms and is called antibonding MO. Horizontal lines in the following figure represent the two atomic and the two molecular orbitals and the respective energy of an electron within this orbital.

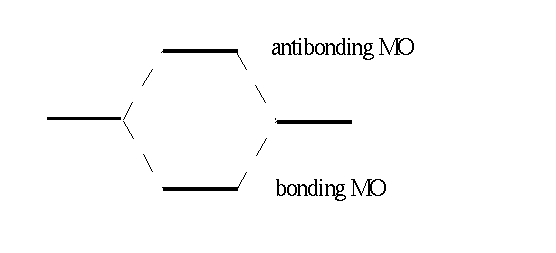
Now we allocate the MOs, beginning with the orbital lowest in energy and having the Pauli principle in mind. For H₂ we obtain wave funcion σ_g(1) for one electron and σ_g(2) for the other. For the total wave function our approach yields:

The first two terms indicate that both electrons are located near different nuclei (for H: protons) whereas the last two terms describe two electrons located around one single nucleus (A resp. B). There is another approach by Heitler-London that just ignores the last two terms argueing that the repulsion between the two electrons will make this situation quite improbable (i.e. there is an interdependence between the electrons). But occasionally, this happens. Therefore, MO and Heitler-Londer's are two extreme approaches and a superior description is to be found between the two, e.g. in the so-called ionic approach with c as variation constant:

1. The energy of Φ_A and Φ_B for the single atoms A and B ought to be similar. Therefore, the valence orbitals of two atoms are able to combine whereas for electrons from the valence shell and electrons from inner shells, no relevant combination is found. The latter are of very low energy.
2. The product Φ_A·Φ_B ought to be large, a point which is often referred to as "principle of maximal overlap".
3. The functions Φ_A and Φ_B ought to have the same symmetry with respect to the molecule's axis.

An overview to possible and impossible combinations of atomic orbitals of the types s, p and d is given in the following table:
 

The figure below depicts the additive and subtractive combination of p-orbitals to give two MOs. By convention, direction z is in line with the axis between both nuclei. (Click here for further examples of MOs and for the specific cases of 1s+1s and 2s+2s. Subtracting one p_z orbital from another yields the bonding LCAO σ_g, whereas the linear combination obtained by adding the two p_z orbitals leads to the antibonding orbital σ_u. From combinations of p_x or p_y orbitals π-orbitals emerge; thus, these orbitals are doubly degenerated. An additive combination of p_x or p_y AOs produces a marked overlap and therefore a bonding MO (π_u). In contrast, subtractive combination gives rise to antibonding MOs (π_g).

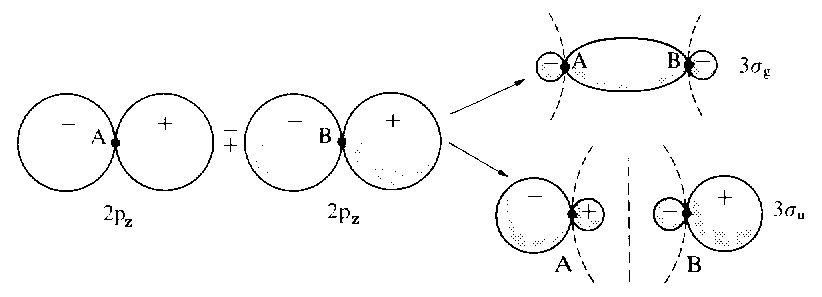From combinations of two 2pz atomic orbitals one bonding and one antibonding molecule orbital emerge, labelled as 3σg and 3σu. Axis z points to the right. Note the signs of the lobes and the way they combine. Dashed lines indicate nodal planes.

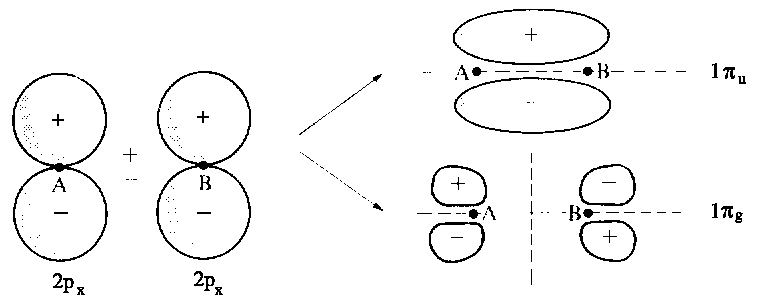Combination of two 2pxatomic orbitals gives as well rise to one bonding and one antibonding molecular orbital, labelled as 1πu and 1πg. The direction denoted as x is orthogonal to the axis between the nuclei. Note the signs of the lobes. In contrast to the previous combination of two pz atomic orbitals now addition of the AOs yields a bonding MO. Dashed lines indicate nodal planes. πu and πg are doubly degenerated as analogous linear combinations are possible with 2py atomic orbitals.

The symbols for classification of molecular orbitals are similar to those used for atomic orbitals. The symbols s, p, d, ... for atoms correspond to σ, π and δ and refer to the angular momentum of the electron with respect to the axis between the two nuclei and to symmetry of the molecule orbital.

• The symmetry operation of rotation does not affect a σ-molecular orbital (e.g the MOs of H₂⁺). The orbital's distinctive feature is axial symmetry;
• A π molecular orbital consists of one positive and one negative lobe on the two sides of a nodal plane. Rotation by 180° changes but the sign of the wave function's amplitude;
• A δ molecular orbital emerging from d_xy atomic orbitals with nuclei A and B as centres shows two nodal planes. These planes divide the orbital in four lobes. Therefore, rotation of the orbital by 90° changes the sign the wave function. Respective greek letters denote as well the higher MOs and the analogy with latin letters for AOs is kept.

• for a σ-MO (λ = 0) the projection of the angular momentum is 0, thus h;
• for a π-MO (λ = 1) the projection is 1h;
• for a δ-MO (λ = 2) the projection is 2h.

With the numbers in front of the symmetry symbol, molecular orbitals of one symmetry are classified with respect to their energy. The higher the number is, the higher is the energy of an electron within this state.

The sequence of MO energies implies structural properties of molecules in a similar way the energy levels of AOs are used to explain the properties of atoms. The currently available data support the following succession of molecular orbitals:
 

For atoms of the second row of the periodic table forming two atomic molecules, the σ_g-MO is always below the π_u-MO. Note that π-MOs appear doubly degenerated. 1π_u is therefore used as an abbreviation for the pair of orbitals 1π_xu and 1π_yu that evidently come from the p_x- and the p_y atomic orbital.

Now we are able to use the succession of MOs to describe homonuclear two atomic molecules. The electrons are distrubuted among the orbitals according energy and the Pauli principle. Due to degeneracy, up to four electrons are allocated to the π level. We already know that the two electrons of the hydrogen molecule H₂ occupy the bonding MO, thus the molecules electronic configuration is (1σ_g)². If we continue our consideration with He₂⁺, we would expect the ground state configuration (1σ_g)²(1σ_u) and He₂ would have (1σ_g)²(1σ_u)². In fact, the molecule He₂ is found to be instable in its ground state whereas it is stable in configurations with one electron in a molecular orbital of higher energy, e.g. in a configuration like (1σ_g)²(1σ_u)(2σ_g)).

The instability of He₂ is one example of the general rule that occupation of both the bonding and the respective antibonding molecular orbital does not yield a chemical bond; in fact the antibond wins slightly over the bond because the splitting of the two involved atomic orbital energy levels is not perfectly symmetric.

The MO description tends to ignore the inner shell electrons and descriptions of electronic configurations just care for the former valence electrons. For example Li₂ with two valence electrons is described with the inner shell electrons as

Li₂ [ (1σ_g)²(1σ_u)²(2σ_g)²]

or, shortly by introducing capital letters for complete shells

Li₂ [ KK(2σ_g)² ]

In a similar manner, we describe the electronic configuration of fluorine F₂

F₂ [ KK(2σ_g)²(2σ_u)²(1π_u)⁴(3σ_g)²(1π_g)⁴ ],

where (1π_u)⁴ denotes the degenerated pair of (1π_xu)²(1π_yu)². 2σ_g and 2σ_u as well as 1π_u and 1π_g are pairs of bonding and antibonding MOs. Therefore, of the 14 valence electrons only the pair of electrons in (3σ_g)² are regarded as bonding and this corresponds to the finding of a single bond of σ-type in the molecule.

The total configuration (term symbols) is derived from the electronic configuration. Clicking will deliver details of the procedure and a summary for the term symbol notation. These term symbols consist of greek capital letters Σ, Π, Δ, ... (indicating the projection of the total angular momentum respective the axis between the two nuclei), the subscript g or u (for molecules with a centre of symmetry) and a preceding superscript (indicating the spinmultiplicity 2S+1 for the total spin S). The sign superscript for Σ states indicates the effect of reflecting the wave function on an arbitrary plane that contains both nuclei.

Examples:
²Π_u   total spin = 1/2; total angular momentum = 1; inversion changes the wave function's sign
³Σ_g^-  total spin = 1; total angular momentum = 0; inversion does not change the wave function's sign

First: The notions of single, double and triple bond refer to the number of pairs of electrons with an effective contribution to bonding. σ and π denotes the type of bond. Typical electronic configurations are

single bond σ², double bond σ²π², triple bond σ²π⁴.

For atoms of the first two rows, no other bonds exist. In contrast, for heavier atoms we face additional possibilities. E.g. there are strong bonds between metal atoms with the configuration σ²π⁴δ² that would be regarded as quadrupole bond.

Second: The principle of maximal overlap predicts that π atomic orbitals with their lobes orthogonal to the axis between the nuclei will not overlap to the same extent as σ atomic orbitals where the distribution of charge is colinear with the axis. Therefore, π bonds are weaker than σ bonds. In analogy, the repulsion caused by antibonding σ orbitals exceed the attraction due to bonding π MOs.

Third: Hund's rule for the allocation of electrons in degenerated MOs (e.g. π_x, π_y) applies in the same way as with AOs in atoms. Thus, for molecular oxygen O₂, all levels up to 1π_u are occupied and electrons with parallel spin in the degenerated 1π_g levels cause the triplett ground state (S = 1).

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.