Hybrization

Now we want to consider the example of Lithiumhydride LiH and apply the LCAO description of molecular orbitals. Ab initio calculations (derived from the self consistent field approach) with a minimal basis (i.e. the Li atom with 1s-, 2s- and 2p-atomic orbitals and Φ_1s, Φ_2s and Φ_2p as wave function and a hydrogen wave function Φ_H) produce (neglecting a minor involvement of Φ_1s) according to Ransil (1960) the following molecular orbitals

1σ ≈ Φ_1s
2σ  ≈  0.323 Φ_2s + 0.231 Φ_2pz + 0.685 Φ_H

LiH [(1σ)² (2σ)²]

Thus, in lithium hydride we find an inner shell (1σ)² that is almost identical with the respective atomic orbital, and a bonding 2σ-MO occupied by two electrons. The 2p-AO of lithium needs to be introduced because the 2p-AO is only slightly higher in energy and the condition of similar energies for combining AO is met in the same way as it is with the 2s-AO. Thus, we shall combine all atomic orbitals of a certain energy level and solve the respective secular equation. The solution above has been obtained exactly in this way.

Nevertheless, there is still an opportunity to cling to the simple principle where molecular orbitals emerge from an overlap between two orbitals and that both sides introduce just one orbital. In the following form, the equation allows for this.

2σ  =  0.397 (0.813 Φ_2s + 0.582 Φ_2p) + 0.685 Φ_H

Φ_hybrid  =  0.813 Φ_2s + 0.582 Φ_2p

have been multiplied in a way that the function is normalized. In general, we require that

∫(a Φ_2s + b Φ_2p)² dτ =  a² + b²  = 1

Note that, as the hybrid orbital have the nucleus as a commom centre, "mixed" elements of the kind ∫&Phi_2sΦ_2pdτ  disappear. To characterize such an sp-hybrid, the population, i.e. a² and a², is often introduced in the form of a superscript: s^0.661p^0.339 (a=0.813, a²=0.661 and b=0.582 b²=0.339). More and more often, we find an notation normalized with respect to s, i.e. in our example sp^0.51. Thus the bonding MO of LiH emerges from an overlap between the hydrogene 1s- and the lithium hybrid orbital (h) where the contribution of p is the 0.51-fold of the contribution of s.

2σ =  0.397 Φ_h + 0.685 Φ_H

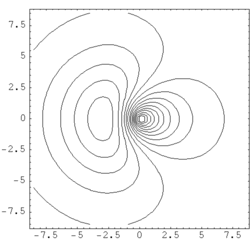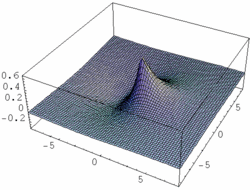
Fig. 1: Contour map of a hybrid orbital formed by an s-p combination of atomic orbitals. The nodal plane lays beside the nucleus' position which is the origin of the coordinate plane

The term hybridization in general relates to a combination of atomic orbitals of one single atom. In MO calculations, there are more cases where such hybrid orbitals appear than cases where they are absent. Introducing hybrid orbitals in the LCAO description of a molecule allows us to receive a bonding (or anti-bonding) MO by combining one orbital from one atom with another orbital of the other atom, where the term "orbital" represents one of our well known 1s, 2s, 2p,... atomic orbitals or a hybrid orbital. Therefore, introducing hybridization widens and improves the applicability of the LCAO approach. Fig. 1 depicts an hybrid orbital and proves such orbitals to be especially appropriate for a large overlap of orbitals. In turn, an enlarged overlap favours the stability of the molecule. The partial characteristics of an p-orbital in the hybrid model of lithium ease an overlap with the 1s orbital of hydrogen. As the coefficients are found by the variation theorem which introduces the requirement of minimal energy, hybridization lowers the energy of the bonding MO, i.e. the bond gets stronger. In addition, the wave function is improved. The concept of hybridization yields a better description of molecules like lithiumhydrid, even without the respective calculations. Such calculations will not be obligatory unless the coefficients are needed.

Thus, a hybrid orbital is a linear combination of orbitals of one single atom. To an sp hybrid orbital for example, s and p orbitals the atom contribute to the same extent. (see Fig .1). An electron in this state displays 50% s- and 50% p-character. In our example of LiH, the weight of the 2s function was somehow higher than that of the 2p. It was 0.661:0.339 ≈ 1.95:1 instead of 1:1. An sp³-hybrid displays 25% s- and 75% p-character (i.e. s- and p-orbitals contribute with 1 : 3 to the hybrid). Likewise, an sp³d² hybrid is an orbital to which s-, p- und d-functions contribute in the relation of 1:3:2. In general, N atomic orbitals yield N hybrid orbitals orthogonal to each other. There are

• two orthogonal sp orbitals
  (Ψ and |Ψ|² as 3D and contour plot)
• three orthogonal sp² orbitals
  (Ψ and |Ψ|² as 3D and contour plot)
• four orthogonal sp³ hybrid orbitals
• six sp³d² hybrid orbitals.

The shape of hybrid orbitals is recieved by constructive and destructive interference of the involved atomic orbitals. The large lobes of sp hybrid orbitals formed by one s and one p orbital point in opposite directions. The higher the weight of the p component, the smaller the angle between the orbitals of this type. The four sp³ hybrid orbitals establish the directions found in the tetrahedron, the six sp³d² orbitals in the directions found in the octahedron. The construction of hybrid orbitals is done in a way that the orbitals point in the direction of molecular bonds (respectively in the direction of a non-bonding orbital). As any of the mentioned hybrid orbitals display partial s characteristics, none of them shows a nodal plane in the centre of the atom. The nodal planes typical for p- and d- orbital are shifted to an eccentric position (Fig. 1). The following table contains a list of the most important types of hybridization and the spatial distribution of the respective hybrid orbitals.
 

Originally, hybrid orbitals have been introduced in the valence bond theory where all bonds are described as overlap of orbitals of two neighbouring atoms. In the tetrahedral molecule CH₄, the bonds C-H are explained by an overlap of the 1s orbitals of four H atoms with four sp³ hybrid orbitals of the carbon atom.

In a correct description of the trigonal pyramidal molecule NH₃, one of the four hybrid orbitals should differ from the three others. With 107°, the angle between HNH is smaller than the tetrahedral angle. An explanation for this finding is that the ratio of p in the hybrid orbitals establishing the bonds N-H is higher than in a regular sp³ hybrid. For known angles, the following formula allows to calculate precisely the ratio of p in an sp^λ hybrid orbital

cos φ = -1/λ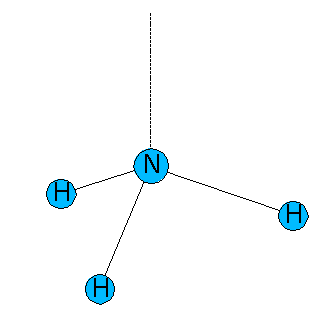

Here, φ is the angle between the NH-bonds. For NH₃ we recieve λ = 3.42. For known angles, the equivalent hybrid orbitals h  =  as + bp can be characterized as the following equations yield the values for a and b.

a²  =  cos φ/cos φ −1	b²  =  1 - a²
a²  =  0.226	b²  =  0.774

The hybridization of other hybrid orbitals are as well mathematically linked to the angle φ. In the case of NH₃, the orbital h' that lays within the three-fold axis of symmetry and to whom we ascribe the non-bonding pair of electrons, emerges as well from combining an s- and p orbitals. As the three hybrid orbitals h display a higher ratio of p (3.42 > 3 in the regular tetrahedron), we expect a minor ratio of p in this fourth hybrid orbital h'.

h'  =  a's + b'p'
a' 2 =  1 + cos φ/1 − cos φ
a' 2 =  0.71/1.29 =  0.547	⇒  b2 = 0.453
0.453 : 0.547 = 0.83	⇒ sp0.83 - hybrid orbital

As the hybrid orbitals of the NH bonds display a higher ratio of p, the nonbonding pair of electrons should occupy an orbital with a higher ratio of s.

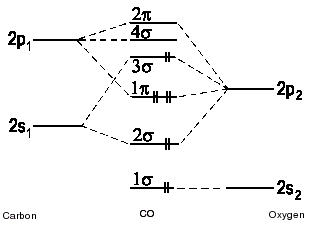Fig. 2a: A correlation diagram the molecule carbonmonooxide CO without hybridization. The highest occupied molecular orbital (3σ) is antibonding. (only valence electrons shown)

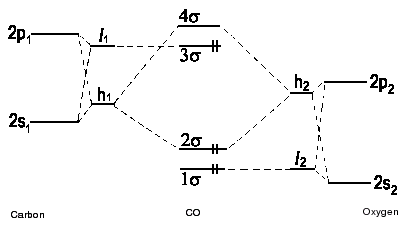Fig. 2b: A correlation diagram for carbonmonooxide CO with hybridization. Due to the pronounced difference in energy between the bonding and the antibonding σ molecular orbitals, the nonbonding pair of electrons is found in the 3σ- molecular orbital. This is in accordance with experimental findings. (To keep the diagram concise, the π orbitals have been omitted.)

The CO molecule is another excellent example for the capability of an approach that takes an hybridization of atomic orbitals into account. Without hybridization, we obtain the correlation diagram in Fig. 2a, where atomic orbitals of similar energy have been paired. Here, the lowest σ orbital is closely related to an oxygen 2s-AO, similar to a nonbonding pair of electrons in the sphere of this atom. The description of next six valence electrons would be (2σ)²(1π)⁴, i.e. one σ bond and two π bonds. Finally, there is a pair of electrons in the antibonding MO (3σ)². Experimental findings which indicate a strong σ bond and a nonbonding pair of electrons located in the sphere of the carbon atom contradict this description of the carbonmonooxide molecule. Fig. 2b depicts the effect of a slight combination between 2s and 2p_z (which displays σ-symmetry). The hybrid orbital h₁ resembles the C-2s orbital and h₂ the O-2p orbital. As both hybrid orbitals are of similar energy and allow a large zone of overlap, the energy splitting between the bonding and the antibonding MOs is strongly enhanced. The remaining l₁ (or 3σ-MO), which is comparable with a C-2p orbital with a contamination of 2s, accepts a non-bonding pair of electrons. As the hybrid orbital h₁ points towards the oxygen atom, l₁ points to the outside. In this model of CO, the antibonding 4σ orbital is empty.

The orthogonal partner of

h₁ = a 2s + b 2p

is

l₁ = b 2s − a 2p.

Carbonmonooxide is able to be bound by transition metal ions, a finding that is easily to be explained by the lone pair of electrons on the carbon side of the molecule that interacts the metal cation. The anion CN⁻ and the cation NO⁺ are isoelectronic to carbonmonooxide. As well, they are found in complex compounds with transition metal elements and bonding in these diatomic species is explained by an analogous electron configuration.

The previous considerations should underline the importance of hybridization in a qualitative theory of chemical bonding. In advance, this concept provides the most important results of a complete wave mechanical calculation: Pairing of orbitals of similar energy and suitable geometry.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.