Selection rules for pure rotational spectra

A molecule must have a transitional dipole moment that is in resonance with an electromagnetic field for rotational spectroscopy to be used. Polar molecules have a dipole moment. A transitional dipole moment not equal to zero is possible.
 

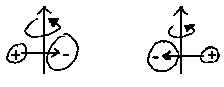z. B. HCl

	symmetric stretch mode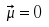
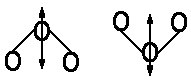	bending mode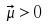
	antisymmetric stretch mode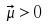

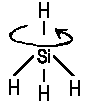With high rotational speed, an originally spherical symmetry of a molecule is distorted.

In contrast, no rotational spectra are displayed by homonuclear diatomics; the same is true for spherical tops. Nevertheless, certain states of a such molecules allow unexpected interactions with the electromagnetic field; i.e.

• some vibrations, that introduce a time-dependent dipole moment
• high rotational speeds that cause some distortion of an originally spherical symmetry. A (weak) dipole moment emerges.

For a symmetric top, an existing dipole moment is always parallel to the molecule's axis. Thus, with respect to this axis, no changes of the rotational state occur.
 

ΔK = 0

For transitions J + 1 ← J, an equation of the following kind rules the wavenumbers of absorbances to occur.

ν = B(J + 1)(J + 2) - BJ(J + 1)  
ν = 2B(J + 1)  with   J = 0, 1, 2...

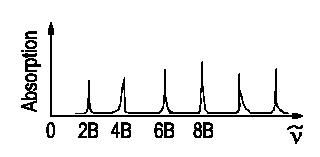The distance between two lines is constant. Δν = ν(J) −ν(J−1) = 2B. We are then able to determine the bond's length r as I = µr2.

For high rotational speeds and centrifugal forces that stretch a molecule, a more accurate equation for ν is

ν = B(J+1)(J+2) - D(J+1)2(J+2)2 - BJ(J+1) + DJ2(J+1)2

ν = 2B(J + 1) - 4D(J + 1)3

i.e., the distance between the lines

Δν = ν(J) - ν (J − 1)

Δν = 2B - 4D(3J2+ 9J + 7)

decreases with J. Thus, the centrifugal constant D for diatomic molecules is in connection with the wavenumber ν_S that corresponds with the molecule's vibration.

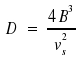
Conversely, D provides information on ν_s. Of course, the intensity of an absorption is dependent on the transitional dipole moment and on the occupancy of the initial and the final state.
 
 

  Contents  

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.