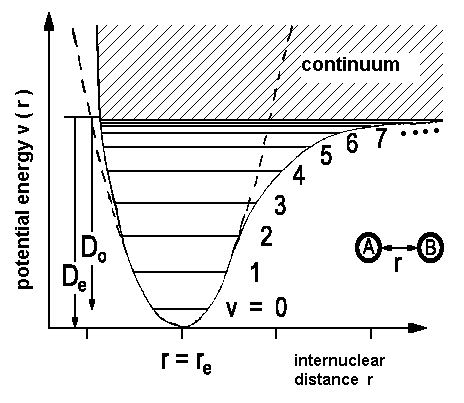
In a previous chapter, we already used the energy levels and wave functions for an harmonic oscillator to understand diatomic molecules. Because changes of
the electric dipole moment always occur when matter interacts with light, no
vibrational spectra are found for homonuclear molecules. For heteronuclear
molecules, the selection rules of the harmonic oscillator are applicable.
| Δv = ± 1 | |
| E = |
v = 0, 1, ... |
It is possible to expand the dipole moment µ with the internuclear distance as its origin. This distance, appearing as r in the potential diagram above, is denoted as variable z in the following mathematical treatment.
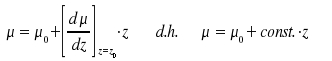
The eigenfunctions
of the harmonic oscillator are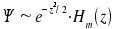 
. Thus, we obtain
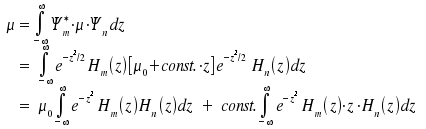
Due to the orthogonality of the Hermite polynomials, the only situation where the first term contributes to µ is if m = n. This condition is incompatible with the fact that any transisition means that m ≠ n. To evaluate the second integral we use the following relation
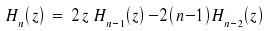
Substitution n+1 for n and transformation yields the equation z · Hn(z) = ½ Hn+1(z) + n · Hn-1(z). By inserting into the second integral we obtain
 |
+ |  |
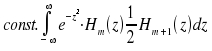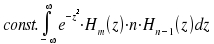| not equal zero only in cases where m = n + 1 |
not equal zero only in cases where m = n - 1 |
Therefore, a change of one for v is needed to have transitions between two states.
Improved mathematical descriptions of the vibrational states are based on the Morse potential V(r)
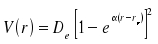
where De is the minimal value of the potential and is found for x = xe and
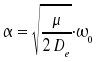
With the potential curve, the energy levels obtained are
 |
 |
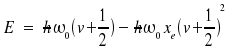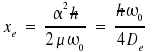Regrettably, the Morse potential cannot often be applied in many problems, Schroedinger's equation has to be solved anew. In practice, to calculate molecular constants from experimental data, an equation of the following type is used.
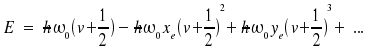
Note that ωexe and ωeye are regarded as one single constant instead of a product. The counterpart of the distance between two levels is a line at some position within the spectrum. The energies respective transitions v + 1 ← v are:
 |
 |
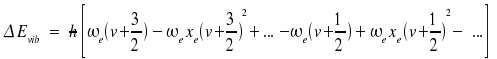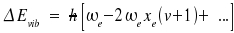The frequency for the so-called fundamental that reflects a transition v = 1 ← v = 0 therefore is
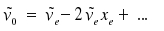
The zero point energy Ev=0 appears shifted too
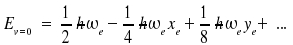
Examples (wavenumbers in cm-1)
| molecule | ~νe / cm-1 | ~νexe / cm-1 | ~ν0 / cm-1 | re / pm | remark |
| H2 | 4401 | 121 | 4159 | 74,1 | ← inactive within IR |
| HCl | 2991 | 52,8 | 2885 | 127,5 | |
| N2 | 2359 | 14,3 | 2330 | 109,8 | ← inactive within IR |
| I2 | 214 | 0,61 | 212,8 | 266,6 | ← inactive within IR |
| OH | 3738 | 84,9 | 3568 | 96,97 |
As, compared with kT at room temperature, the vibrational energies
generally are quite high. Transitions related to absorption only occur between
v = 0 and v = 1. On the other hand, chemical reactions may
form molecules in high vibrational levels and emissions from such levels need to
be considered. For example, the origin of some weak luminescence in the upper
stratosphere is an excited OH-radical emerging from the H + O3 → OH(v
= 9) + O2.
Another two useful equations:
The molar bond dissociation enthalpy
ΔHm and dissociation energy D0 are related by:
 |
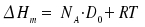NA: Avogadro's number |
The difference between the dissociation energy D0 and the depth De of the potential equals the zero point energy.
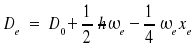
Harmonics
Due to anharmonicity, spectra may display lines forbidden by the selection
rule Δv = ± 1. The intensity of these harmonics is weaker. Due to
lasers and their high energy flux, it has been possible to stimulate harmonics.
The table below lists the spectral position of some harmonics of the OH radical.
σ0 represents the relative intensity of the line; the fundamental
line's intensity is set to 100.
| Example: Transition probabilities for the OH radical | ||||
| v' ← v'' | ν / cm-1 | λ / nm | σ0 | spectral range |
| 1 ← 0 | 3568 | 2803 | 100 | infrared |
| 2 ← 0 | 6966 | 1436 | 16 | |
| 3 ← 0 | 10195 | 980 | 0.5 | |
| 4 ← 0 | 13253 | 755 | 0.03 | visible |
| 5 ← 0 | 16142 | 619.5 | 0.01 | |
Vibrations of polyatomic molecules
Polyatomic molecules may vibrate in 3N-5 different ways if they are linear and in 3N-6 different ways if they are not. Therefore, the carbon dioxide molecule has four degrees of freedom for vibrations (the molecule can bend in two directions); whereas the water molecule has only three. Normal modes of vibration are mutually independent motions of groups of atoms; any one mode may be excited without leading to excitation of the others.
For more complex molecules it is advantageous to classify the normal modes of vibration according to symmetry in point groups (e.g. C2v for water). These aspects dictate whether vibrations are involved in transitions in the IR range of the spectrum, i.e. if the vibration is IR active.
The diagram below shows the vibrational states of the water molecule and the
respective energies. Each state is IR-active and, of course, in none of them
vibrational motions affect the centre of mass.
 |
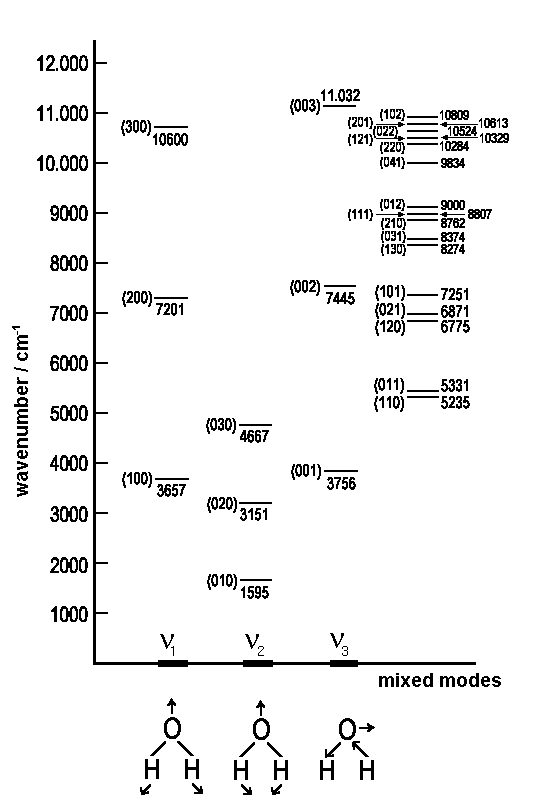| Vibrational levels of gazeous water in cm-1. The numbers in brackets (v1,v2,v3) characterize the pure and mixed modes of vibration |
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.