Der schwingende Rotator
Das Trägheitsmoment Ie eines nichtschwingenden zweiatomigen Moleküls ist Ie = µre2.
Aufgrund der Schwingung erfolgt eine Mittelung über die quadratische Auslenkung r, Iv = µ< r2>; dadurch wird Iv größer (µ: reduzierte Masse).
Anschauliche Rechnung, r = re ± s :
Iv = µ<r2> = µ<(re ± s)2> = µre2± 2<µsre> + µ<s2> = µre2 + µ<s2>
(± 2 <µsre> mittelt sich raus), was offensichtlich größer als µre2 ist.
Die Rotationskonstante B wird daher schwingungsabhängig:
mit Schwingung: Bv = h/4πcµrv2
ohne Schwingung Be = h/4πcµre2.
Bv < Be
Man erhält zur Beschreibung von Bv folgenden Ansatz:
Bv = Be - αe(v + ½) und dto. Dv = De - βe(v + ½)
wobei αe, βe
kleine
Korrekturgrößen sind.
| Beispiel HCl: | ||||
| Be | Bv = 0 | Bv = 1 | Bv = 2 | Bv = 3 / cm-1 |
| Be = 10,5934 | 10,44 | 10,13 | 9,83 | 9,52 |
| De = 5,32 · 10-4 | ||||
| αe = 0,3072 | ||||
| βe = 7,51 · 10-6 | ||||
Es soll im folgenden die Rotation der Elektronen um die Molekülachse
vernachlässigt werden. Die Energie eines rovibronischen Zustandes
ist dann [alles in cm-1]:
| E = Evib + Erot = we(v + ½) - wexe(v + ½) + BvJ(J + 1) - DvJ2(J + 1)2 |
Die Energiedifferenz für einen Übergang v' ←
v, v' = v + 1 (noch ohne J-Auswahl) ist dann unter Vernachlässigung
der Zentrifugaldehnung D:
| ΔE = | we - 2wexe(v + 1) | + {Bv'J'(J' + 1) - BvJ(J + 1)} |
| ½¾¾¾¾¾¾½
¯ |
||
| n0 |
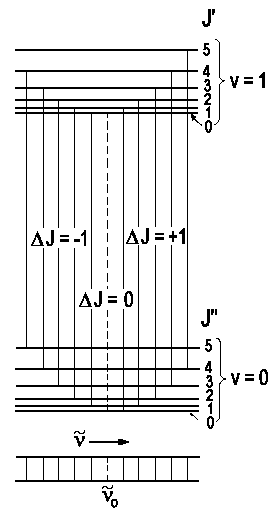
Für ΔJ = + 1, sogenannter R-Zweig,
also J + 1 ← J gilt:
| n = n0 + 2Bv' + | (3Bv' - Bv) | J - | (Bv - Bv') J2 | mit J = 0, 1, 2, ... |
| (>0) | (>0) |
Für ΔJ = -1, sogenannter P-Zweig, also J - 1 ← gilt:
n = n0 - (Bv + Bv') J - (Bv - Bv') J2 mit J = 1, 2, 3, ...
Der Abstand zwischen zwei aufeinanderfolgenden Linien J, J+1 ist
Dn (R-Zweig)
= 2(2Bv' - Bv) - 2(Bv - Bv')
J (abnehmend)
Dn (P-Zweig)
= 2Bv + 2(Bv - Bv') J
(zunehmend)
Der Abstand zwischen zwei Linien beträgt danach ungefähr 2B, falls Bv » Bv' . Der Abstand zwischen 1. Übergang im R-Zweig und P-Zweig ist aber
Dn (R-P-Zweig) ≈ 4Bv
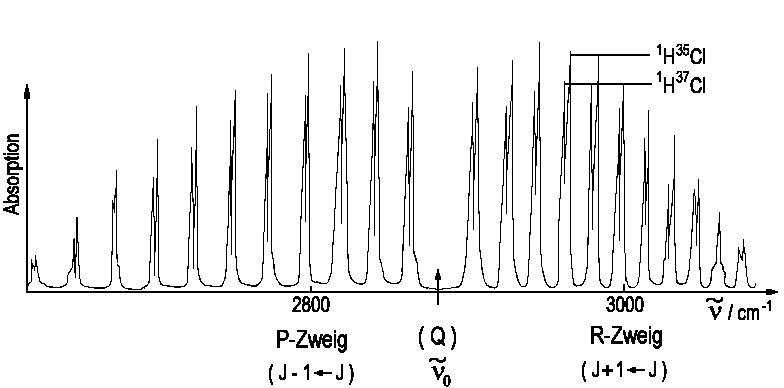
Fast alle zweiatomigen Moleküle zeigen ein solches Spektrum mit
R- und P-Zweig. Als Beispiel ist das HCl dargestellt. Die Aufspaltung der
Linien resultiert aus der Verwendung eines natürlichen Isotopengemisches,
da sich die reduzierte Masse µHCl um 0,15% ändert.
Dies bewirkt im wesentlichen einen Änderung der Schwingungsfrequenz,
Dw»
2cm-1.
 |
||
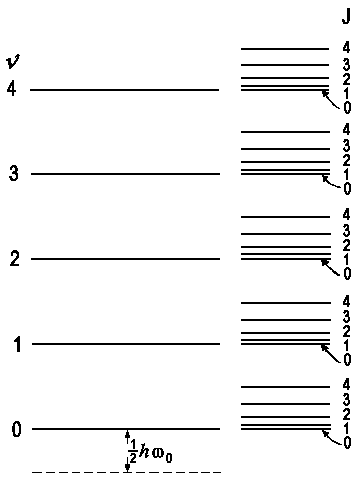
| Vibrationsniveaus
Ev = (v + ½) hw0 |
Rotationsniveaus
Er = B · J (J + 1) |
 |
 |
||
| Vibrations- und Rotationsenergieniveaus eines zweiatomigen Moleküls |
P-branch
R-branch
ΔJ = −1 ΔJ = +1 |
|
|
|
||
Es gibt auch Moleküle, die ein Spektrum aufweisen, bei dem in der
Bandlücke zwischen P- und R-Zweig zusätzliche Linien auftauchen.
Dies ist der sogenannte Q-Zweig, für den ΔJ
= 0 gilt. Natürlich muss die Rotation erhalten bleiben, d.h.
solche Übergänge sind nur möglich, wenn sich die Rotationsachse
ändert (ΔK¹ 0), bzw. wenn die elektronische
Bewegung für eine Kompensation sorgt. So tritt bei rovibronischen
Spektren zweiatomiger Moleküle der Q-Zweig nur dann auf, wenn die
Elektronenbewegung ebenfalls einen Beitrag zum Gesamtdrehimpuls liefert.
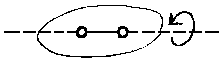 |
| Projektion der Elektronenrotation auf die Molekülachse: Λ = 0, 1, 2, ... |
Man kennzeichnet die Größe dieses Drehimpulses als Projektion
auf die Kernverbindungsachse durch die Quantenzahl Λ.
Für Λ = 0 bleibt alles beim alten. Der
Gesamtdrehimpuls des Moleküls (also Kernrotation + Elektron) ist |J|
≥
|Λ|.
Die Energieniveaus sind dann analog zum symmetrischen
Kreisel.
| EJ = | BJ(J + 1) + | (A - B) Λ2 |
| Kernrotation | | |
| Elektronenbewegung A >> B |
Die Auswahlregeln für Λ ¹ 0 ändern sich; es ist jetzt neben
Ein Beispiel ist NO; allerdings gibt's auch hier Spin-Phänomene, die eine detaillierte Betrachtung verkomplizieren. Vernachlässigen wir einmal den Spin, wie sieht dann so ein Q-Zweig (ΔJ = 0) aus?
E(v',J) - E(v,J) = n0 + Bv'J(J+1) + (A-Bv')Λ2 - BvJ(J+1) - (A-Bv)Λ2
n0 (Q-Zweig) = n0 - (Bv-Bv')J(J+1) + (Bv-Bv')Λ2
Da Bv ≈ Bv' müssen alle Q-Linien sehr dicht beieinander liegen.
Die Auswahlregeln für den symmetrischen Kreisel lauten für
die sogenannte
Parallelbande (ΔK = 0)
für K = 0, ΔJ = ± 1
(wie 2atom. Molek.)
für K ¹ 0, ΔJ
= 0, ± 1 (wie 2atom. mit Elektr.)
Senkrechtbande (ΔK = ± 1)
ΔJ = 0, ± 1
Die Intensität der rovibronischen Linien hängt natürlich von der Übergangswahrscheinlichkeit und den Besetzungszahlen NJ der betroffenen Zustände ab. Falls nur v = 0 populiert ist →
I ˜ NJ · |µJ'J|2
I ˜ NJ · SJ
SJ: Hönl-London-Faktoren
Für den einfachen Rotator sind die Übergangswahrscheinlichkeiten für große Rotationen unabhängig vom Übergang, d.h. die Besetzungszahlen im Vibrationsgrundzustand (J-Verteilung) bestimmen im wesentlichen die Intensität. Nach Boltzmann gilt:
NJ ˜ (2J+1) e-Erot/kT = (2J+1)e-BJ(J+1)/kT
Das Maximum der Besetzungszahlen können wir abschätzen, falls der Abstand zwischen den Rotationsniveaus << kT ist, was für T ≈ 300 K immer der Fall ist. Dann setzen wir J als Variable x an und suchen das Maximum:
dNx/dx = 0 d[(2x+1)e-Bx(x+1)/kT] /dx = 2e-Bx(x+1)/kT - B/kT(2x + 1)2e-Bx(x+1)/kT = 0
→ xmax = -½ + (kT/2B)½ = Jmax
Jmax ≈ (kT/2B)½ Beispiel: Jmax(HCl) ≈ 2 - 3; Jmax(I2) ≈ 50
Bei thermischen Verteilungen kann man daher aus den Linienintensitäten
die Temperatur bestimmen, z.B. in der Stratosphäre. In chemischen
Reaktionen werden die Produkte häufig mit einer Zustandsverteilung
gebildet, die völlig von einer Boltzmannverteilung abweicht. Aus den
Linienintensitäten kann hier auf die Besetzungszahl des jeweiligen
Ausgangszustandes geschlossen werden (falls die Übergangswahrscheinlichkeit
bekannt ist). Bei vielen Reaktionen, die HF bilden, wird HF in schwingungsangeregten
Zuständen gebildet. Darüber kann der Ablauf einer Reaktion detaillierter
(auf mikroskopischem Niveau) verstanden werden, was John
C. Polanyi 1986 den Nobelpreis eingebracht hat (neben D.R
Herschbach und Y.T.
Lee).
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.