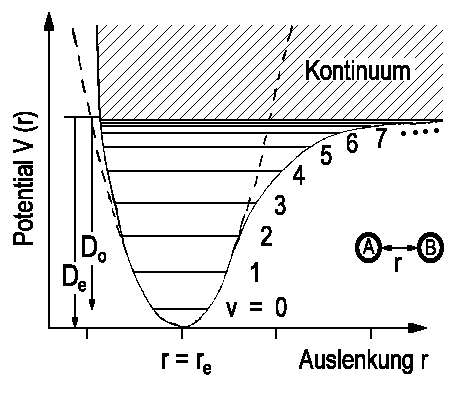
Die Energieniveaus und Wellenfunktionen für eine harmonische Schwingung haben wir bereits als Näherung für die Potentialkurve eines zweiatomigen Moleküls kennengelernt. Da sich das elektrische Dipolmoment des Moleküls während der Schwingung ändern muss, besitzen homonuklare Moleküle kein Schwingungsspektrum. Für heteronukleare Moleküle erhält man die Auswahlregeln in harmonischer Näherung
| Δv = ±1 | |
| E = |
v = 0, 1, ... |
Das Dipolmoment µ kann bezüglich der Abstandskoordinate r, die wir im folgenden mit z bezeichnen wollen, entwickelt werden:
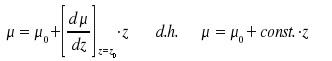
Die Eigenfunktionen
des harmonischen Oszillators sind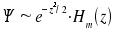 
. Wir erhalten also:
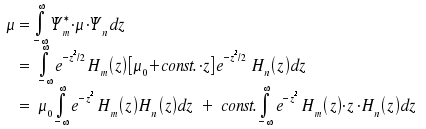
Der erste Term liefert wegen der Orthogonalität der Hermiteschen Polynome nur einen Beitrag für m = n, . Bei einem Übergang ist jedoch m ≠ n. Für die Auswertung des zweiten Integrals ziehen wir die Beziehung
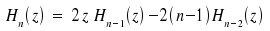
heran. Ersetzen n → n+1 und umformen nach: z · Hn(z) = ½ Hn+1(z) + n · Hn-1(z) ergibt nach Einsetzen für das zweite Integral:
 |
+ |  |
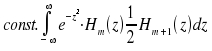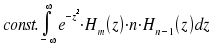| nur dann ungleich Null, wenn m = n + 1 | nur dann ungleich Null, wenn m = n - 1 |
D.h. die Quantenzahl muss sich für den Übergang von einem zum anderen Niveau um 1 ändern.
Eine bessere Beschreibung des Potentials erfolgt durch das Morsepotential
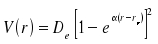
wobei De die Tiefe des Potentialminimums, an der Stelle xe ist und
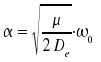
Mit diesem Potential erhält man die Energieniveaus
 |
 |
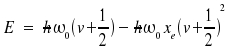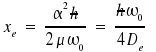Leider hat das Morsepotential keine allgemeingültige Aussagekraft; vielmehr muss die Schrödinger-Gleichung für jedes Problem neu gelöst werden. Zur Beschreibung der experimentellen Daten wird die allgemeine Gleichung
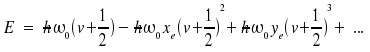
genutzt, wobei die Größen ωexe, ωeye, ... jeweils als eine Konstante (und nicht als Produkt) angegeben werden. Der Abstand zwischen zwei Niveaus (also das Spektrum) ist dann (v + 1 ← v):
 |
 |
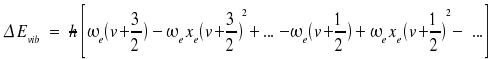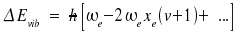Die Wellenzahl ~ν0, bei welcher die Signale für die Übergange zwischen v = 1 und v = 0 ("Grundschwingung") erscheinen, ist demnach hω = hc~ν)
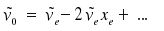
Die Nullpunktsenergie Ev=0 ist ebenfalls verschoben:
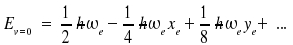
Die folgende Tabelle listet die Molekülschwingungsparameter ~νe und ~νexe in Form von Wellenzahlen, die Wellenzahl für den Übergang v = 0 nach v = 1 sowie den Gleichgewichtsabstand re für eine Reihe zweiatomiger Moleküle auf.
|
|
|
|
|
||
|
|
|
|
|
|
← IR-inaktiv ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
← IR-inaktiv ! |
|
|
|
|
|
|
← IR-inaktiv ! |
|
|
|
|
|
|
Da die Schwingungensenergie im allgemeinen sehr groß gegen kT bei Raumtemperatur ist, finden Übergänge nur von v = 0 nach v = 1 in Absorption
statt. Allerdings kann in chemischen Reaktionen auch ein Produkt in sehr
hohen Schwingungsniveaus gebildet werden und man kann Emissionen aus diesen
Niveaus beobachten.
Z.B. verursacht die Reaktion H + O3 → OH(v = 9) + O2 ein schwaches Leuchten in der oberen Stratosphäre
durch vibronische Übergänge.
Noch zwei nützliche Gleichungen:
Die molare Bindungsdissoziationsenthalpie ΔHm und die Dissoziationsenergie D0 verbindet die Gleichung:
 |
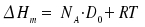NA: Avogadrozahl |
Der Unterschied zwischen der Dissoziationsenergie D0 und der Tiefe De des Potentialtopfes ist über die Nullpunktsenergie gegeben:
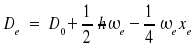
Aufgrund der Anharmonizität können auch Linien auftreten, die nach der Auswahlregel Δv = ± 1 verboten sind. Diese Obertöne besitzen eine schwächere Intensität. Mit Hilfe von Lasern ist es aber aufgrund der hohen Lichtleistung möglich, Obertöne anzuregen.
| Beispiel: Übergangswahrscheinlichkeiten für OH | ||||
| v' ← v'' | ~ν / cm-1 | λ / nm | σ0/normiert auf
1←0 entsprechend 100 |
|
| Infrarot |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| sichtbares Licht |
|
|
|
|
|
|
|
|
|
|
Schwingungen mehratomiger Moleküle
Ein nichtlineares N-atomiges Molekül besitzt 3N-6 Normalschwingungen; ein lineares 3N-5. CO2 hat als lineares Molekül 4 Schwingungsfreiheitsgerade (die Biegeschwingung tritt "doppelt" auf); während Wasser nur 3 Schwingungsfreiheitsgerade besitzt. Bei Normalschwingungen beeinflußt die angeregte Schwingungsmode nicht die anderen Normalschwingungen.
Bei größeren Molekülen ist es zweckmäßig, die Normalschwingungen entsprechend ihrer Symmetrie in Punktgruppen einzuteilen. Das gleiche gilt für die Entscheidung, welche der Schwingungen IR-aktiv sind. In der folgenden Abbildung sind drei Normalschwingungen vom H2O (alle IR-aktiv) angegeben. Der Schwerpunkt des Moleküls muss natürlich bei einer Schwingung in Ruhe bleiben.
 |
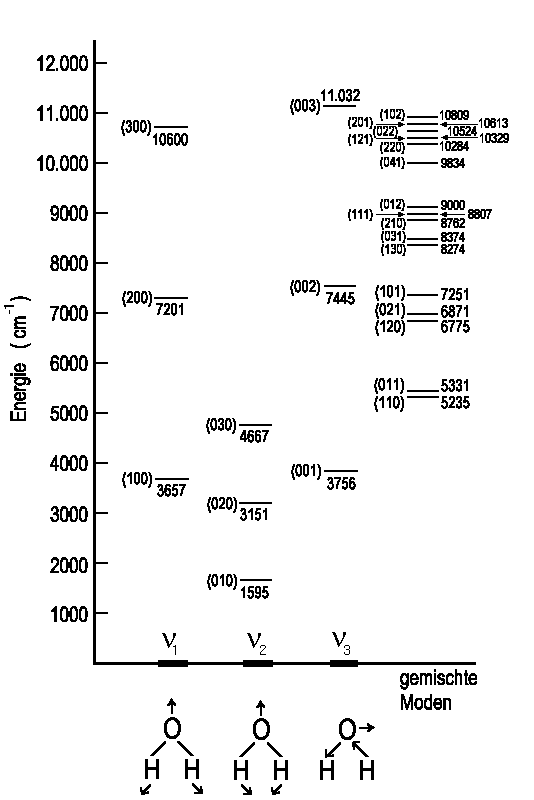| Vibrationsniveaus von gasförmigem Wasser in cm-1. Die Werte in Klammern sind die Vibrationsmoden (v1, v2, v3) |
Home
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.