Symmetry adapted AO - H₂O as an example

Like with diatomic molecules, a consideration of the symmetry of the molecule and the symmetry of involved atomic orbitals yields valuable information on the molecular orbitals. As an approximation to molecular orbitals, we will deal with linear combinations of atomic orbitals. Finding the molecular orbitals is facilitated by introducing the aspect of symmetry. Therefore, we establish "symmetry adapted linear combinations" of atomic orbitals, the so-called symmetry orbitals.

Taking the water molecule as an example, we will illustrate this method. We assume a bent structure with identical distances H-O (questions on geometry are answered by the rules of Walsh). The molecule falls into point group C_2v. The molecular orbitals of H₂O need to show this symmetry and the symmetry operations for C_2v affect these orbitals in the same way the respective irreducible representations are affected. For the mentioned point group, all irreducible representations or symmetry species are one-dimensional; thus the values +1 and −1 in the character table for C_2v indicate whether an MO behaves symmetric or antisymmetric with respect to an operation.
 

C2v E C2 σv(xz) σv'(yz) A1 1 1 1 1 A2 1 1 1 −1 B1 1 −1 1 −1 B2 1 −1 −1 1

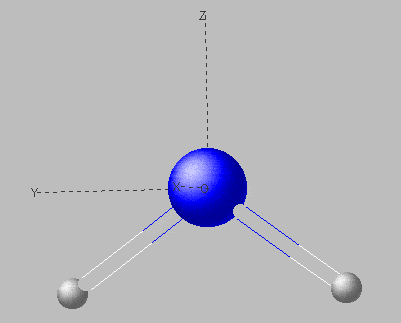An MO of symmetry a₂ (we use minuscules letters for single electron states, i.e. orbitals, and majuscules for the total electronic states of molecules) is therefore symmetric with respect to identity E and a rotation on a two-fold axis C₂ (If there is a distinct axis, it is taken as axis z). In contrast, it is antisymmetric with respect to a reflection on the planes xz and yz. None of the four symmetry operations affects the framework of the molecule itself.
We would be free to choose an orientation with the two hydrogen atoms in the plane xz or in plane yz normally, but, by convention, the second possibility is preferred and both hydrogen atoms lie within the plane yz and axis z bisects the angle H-O-H.

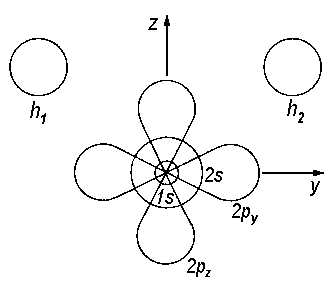Fig.1: Atomic orbitals of the H2O molecule. The orbital px is perpendicular to the plane yz.

The 1s atomic orbitals h₁ and h₂ of both hydrogen atoms contribute to the bonding of the water molecule H₂O. The oxygen atom has electrons in 1s, 2s, 2p_x, 2p_y, 2p_z states. With no regard to inner electrons, we will proceed with the valence shell orbitals denoted s, p_x, p_y and p_z.

With respect to point group C_2v, this set of orbitals is already symmetry adapted as we will demonstrate for the atomic orbital p_x. Applying any of the symmetry operations of the group to the orbital's wave function, we ask whether the sign of the wave function remains constant or changes.

Not surprisingly, identity E leaves the wave function unaffected, therefore 1 is the value noted down for p_x.

E	C2	σv	σ'v
1

Next we imagine a rotation of 180° about the principle axis and check whether there is a change of sign for the respective wave function. As this is the case, the entry below the symmetry operation C₂ p_x is -1.

E	C2	sv	σ'v
1	-1

If the atomic orbital is submitted to reflection on the plane xz, we find the wave function unaltered; therefore the entry below σ_v(xz) is 1.
 

E	C2	σv(xz)	σ'v
1	-1	1

If the atomic orbital is submitted to reflection on the plane yz, we obtain the wave function with reversed sign, therefore the entry below σ_v(yz) is −1.

E	C2	sv	σv'(yz)
1	-1	1	-1

If we compare the values recieved with the entries in the character table of point group C_2v, we recognize it to be identical with one set of characters in a row of the table. This correspondence is fundamental for the classification of orbitals to a certain symmetry species. In our example, b₁ is obtained for p_x. In this way, atomic orbitals and the irreducible representations of C_2v are linked.

atomic orbital	s	px	py	pz
irreducible representation	a1	b1	b2	a1

In contrast to the orbitals of the oxygen atom, the AOs h₁ and h₂ are not symmetry adapted as C₂ or σ(xz) convert h₁ in h₂ and vice versa. But it is easy to recognize that linear combinations like

hs  =  1/√2 (h1 + h2)

ha  =  1/√2 (h1 − h2)

are symmetry adapted. To find the correspondence between the obtained orbital and the symmetry species, we apply the operations. The result is shown in the table below.

atomic orbital	hs	ha
irreducible representation	a1	b2

Using the six symmetry-AOs s, p_x p_y, p_z,h_s and h_a, an equal number of MOs can be formed. Note that identical symmetry is a precondition for such combinations.

As there is only one atomic orbital of symmetry species b₁, it is not introduced in any linear combination and therefore we regarded p_x as a molecular orbital of H₂O as well. Three AOs are of symmetry species a₁. Therefore s, p_z and h_s are combined to yield three molecular orbitals. Finally, p_y and h_a belong to b₂ and are thus combined to yield two molecular orbitals

1a1  =  c11s + c12pz + c13hs

2a1  =  c21s + c22pz + c23hs

3a1  =  c31s + c32pz + c33hs

1b1  =  px

1b2  =  c44py + c45ha

2b2  =  c54py + c55ha

The coefficients c_ik remain to be determined. It is obvious that, for the two b₂ orbitals, these coefficients will have the same sign (we denote this combination with 1b₂) and in the other, they will have opposite signs as orthogonality is imposed on the resulting molecular orbitals. Fig. 2 shows these MOs schematically with hatched areas for positive values and blank areas for negative values of the function.

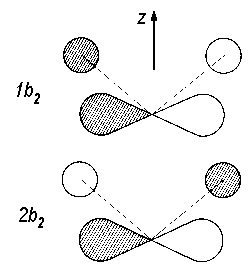Fig. 2: Representation of the orbitals 1b2 and the 2b2 in H2O.

Thus, one of the two molecular orbitals (here 1b₂) is bonding and the other (here 2b₂) is antibonding. Take as a rule for all molecules AB_n that, if there is only one single symmetry orbital from A and one single symmetry orbital from one of the atoms B involved, exactly one bonding and one antibonding MO is formed. If a symmetry species appears exclusively with atom A or with atom B (here b₁ of oxygen), the respective orbital remains as a non-bonding orbital in the molecule.

In a situation where several orbitals of the involved atoms fall in one symmetry species (like a₁ in our example), each pair of atomic orbitals A or B_n usually yields one bonding and one antibonding linear combination. The remaining atom orbitals become non-bonding MOs.

bonding:	1a1	1b2
non bonding:	2a1	1b1
antibonding:	3a1	2b2

Having classified the molecular orbitals, we distribute the electrons according to the building up principle. In a water molecule, we have eight valence electrons, a number that fits with four times one pair of electrons into the bonding and the nonbonding MO. The antibonding MOs remain empty. Here the result of an exact calculation.

We have derived the electronic configuration of the ground state of the water molecule without introducing the aspect of energy. The sequence of MOs in orbital energy is dependent on

1. the energy levels of the orginal atomic orbitals
2. the extent of splitting between bonding and antibonding orbital

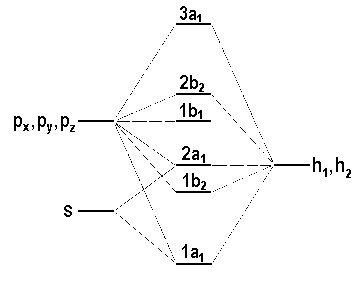Fig. 3: Qualitative representation of the energy of the valence molecular orbitals in the molecule H2O.

If, instead of eight electrons, we had twelve to be distributed over the six orbitals, the number of fully occupied bonding and antibonding orbitals would be equal and no stable molecule could exist. For the stability of a molecule it is normally required that the number of doubly occupied bonding orbitals is equal or higher to the number of doubly occupied antibonding MOs. The difference between these numbers is the number of bonds in the molecule.

An additional important aspect in our context is to consider whether there is at all the possibility to form covalent bonds. If the hydrogen orbitals h₁ and h₂ were of substantially higher energy, we would have linear combinations of approximately this kind

I.e. the electrons were located in the sphere of the oxygen atom and would not contribute to bonding. If we now fill the molecular orbitals 1a₁, 1b₂, 2a₁ and 1b₁, we would recieve the oxygen anion O²⁻ and the hydrogen atoms left as protons. But, due to electronic repulsion, there is a limit for the transfer of electrons. This aspect is not revealed by the scheme of MOs. For compounds AB_n with strongly asymetric distribution of charges, this scheme could lead to wrong conclusions.

In principle, to understand the electronic configuration of H₂O and other molecules of point group C_2V, the following table suggested by G.E. Kimball (J.Chem.Phys. 8, 188 (1940)) suffices.

Kimball table for molecules AB2 of symmetry C2v for atoms B in the plane yz
Atom	C2v	a1	a2	b1	b2
A	s p d	1 1 2	0 0 1	0 1 1	0 1 1
B2	σ π	1 1	0 1	0 1	1 1

The table predicts the way atomic orbitals split and transform to irreducible representations of C_2v. For atom A, the s-orbital becomes a₁, the three p-orbitals become a₁, b₁ and b₂, the five d-orbitals transform to two a₁-orbitals, one a₂, one b₁ and one b₂-orbital. The entries for B₂ display the kind of irreducible representations emerging from σ and π-AOs respectively. The names σ and π are used with reference to the connecting lines between atoms A and B. Orbitals with rotational symmetry about this axis are classified as σ and orbitals with a nodal plane containing this axis as π. For example,

• the positive linear combination for σ (s-electrons: s₁+s₂) yields a₁
• the negative combination yields b₂.
• the positive combination of the two p electrons within the plane yz yields the orbital a₁.
• the positive combinations of p orbitals perpendicular to the plane yz yields an orbital b₁.
• the negative combination of the two p electrons within the plane yz yields the orbital b₂.
• the negative combinations of p orbitals perpendicular to the plane yz yields an orbital a₂.

Applying the Kimball table to the water molecule, we take the s, p and σ states and state that

• two AOs of A, one of B₂, one of A belong to a₁
• no AO belongs to a₂
• one AO of A belongs to b₁
• one AO of A and one of B belongs to b₂.

Often, antibonding molecular orbitals are labelled by an asterisk.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.