Energieverteilung nach Boltzmann

Die Maxwellsche Geschwindigkeitsverteilung gibt uns die Zahl der Moleküle in einem Geschwindigkeitsintervall an, woraus wir natürlich sofort durch Integration die relative Anzahl der Moleküle P(v>v_s) (oberhalb einer Schwellgeschwindigkeit v_s berechnen können:  P(v>v_s) =  _vsò^¥ F(v)dv. Für chemische Reaktionen benötigen wir jedoch die Energie, die notwendig ist, um z.B. eine Energiebarriere zu überwinden, oder um überhaupt eine Reaktion energetisch zu ermöglichen, denn es können natürlich nur die Teilchen reagieren, deren Energie ausreiched ist, um die (eventuelle) Energielücke zwischen Edukten und Produkten zu überwinden. Wir müssen also die Geschwindigkeitsverteilung F(v) in eine kinetische Energieverteilung G(E) umrechnen (Das Symbol G( ) wurde nur gewählt, um die andere mathematische Form dieser Verteilung hervorzuheben) :

Da G(E)dE = F(v)dv gelten muss, erhalten wir durch Einsetzen in die Maxwell-Verteilung:
 

Interessant ist, dass die Masse der Spezies nicht mehr in der Gleichung enthalten ist. Der Verlauf von G(E) als Funktion der kinetischen Energie E (in Einheiten von kT) ist in Abb.1 dargestellt. Für Raumtemperatur T=298 ist beispielsweise kT = 2,5kJ/mol. Eine Erhöhung der Temperatur um nur 30% bewirkt bereits eine deutliche Zunahme der Teilchen, deren Energie grösser als (beispielsweise) 3kT ist.
 

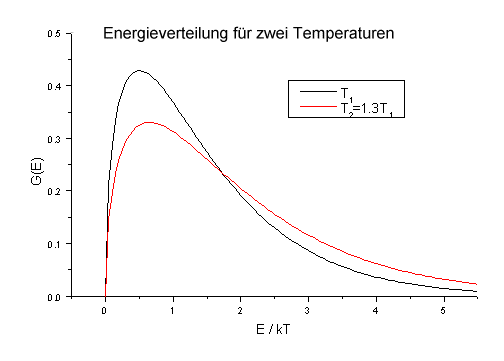Abb.1: Kinetische Energieverteilung nach Maxwell-Boltzmann für zwei unterschiedliche Temperaturen.

Wir wollen uns nun ganz allgemein die molekulare Verteilungsfunktion für die Energie überlegen, wobei wir von den folgenden Voraussetzungen ausgehen:

• Die Wahrscheinlichkeit p(E) für einen molekularen Zustand hängt nur von der Energie E dieses Zustandes ab.
• Wenn zwei weitere Moleküle (1 und 2) die Energie E₁ bzw. E₂ mit der Wahrscheinlichkeit p(E₁) bzw. p(E₂) haben, dann ist die Wahrscheinlichkeit P(E) für die Summe der Energie E = E₁ + E₂ gegeben durch (vergleiche hierzu die Herleitung der Maxwellschen Geschwindigkeitsverteilung):

wobei das (letzte) Gleichheitszeichen gilt, da wir annehmen, dass die Teilchen unabhängig voneinander sind. Nur die Exponentialfunktion erfüllt diese Gleichung (Herleitung):

Die Konstante β bestimmen wir durch Vergleich mit dem obigen Spezialfall: β = -¹/_kT. Den Proportionalitätsfaktor bestimmen wir wiederum durch Normierung, d.h. die Gesamtwahrscheinlichkeit muss 1 sei. Die Wahrscheinlichkeit P(E) ein Teilchen mit der Energie E vorzufinden nimmt also exponentiell mit E ab und ein solcher Verlauf ist in der unteren rechten Abb.2 dargestellt. Die linke Seite der Abb.2 zeigt etwas anschaulicher, wie mit zunehmender Energie die Wahrscheinlichkeit, ein Molekül mit solcher Energie zu finden, abnimmt.
 

Abb.2: Die Wahrscheinlichkeit N(E)/N ein Teilchen bei der Energie E zu finden nimmt exponentiell mit E ab: N(E) ~ e-E/kT (rechts). Die linke Abb. zeigt, wie die Besetzungszahl N(E) bei der niedrigst möglichen Energie Eo am grössten ist und mit zunehmender Energie exponentiell abnimmt.

Wenn wir die Energiewerte kennen, die unsere Teilchen annehmen können, dann ist der Bruchteil ^N(E)/_N der Teilchen, die diesen Energiewert besitzen, gegeben durch:
 

Dank der Quantenmechanik weiss man z.B., dass Moleküle ganz charakteristische Schwingungen besitzen, die wiederum der Identifikation des Moleküls und dessen Strukturaufklärung durch die Spektroskopie dienen. Einem Schwingungstypus können nun einzelne Energien E₀, E₁, E₂,... mit äquidistanten Abständen (idealisierter harmonischer Oszillator) zugeordnet werden.  Mit Hilfe der obigen Gleichung können wir nun ausrechnen, wieviele Moleküle im niedrigsten Schwingungszustand, oder in irgendeinem höher angeregten Zustand sind.
Falls die Teilchen unterschiedliche Zustände einnehmen können, die aber die gleiche Energie haben, dann spricht man von der Entartung eines Zustandes. Der Grad der Entartung, d.h. wieviele unterschiedliche Zustände die gleiche Energie E haben, wird mit g(E) bezeichnet. Ein einfaches Beispiel zur Entartung ist die Knickschwingung des linearen CO₂-Moleküls:  O - C - O. Die Schwingung kann in der Zeichenebene (nach "oben" und "unten") erfolgen oder senkrecht dazu (nach "vorn" oder "hinten"). Die Energie der Schwingung muss gleich sein, also ist die Schwingung zweifach entartet, d.h. g = 2.

Wir müssen diese entarteten Zustände natürlich in unserer Boltzmannverteilung mit berücksichtigen und es gilt ganz allgemein:
 

Dies ist das Boltzmannsche Energieverteilungsgesetz. Wir können nun noch formal die Normierung durchführen:
 

wobei die Grösse Q Zustandssumme (im englischen "partioning function") genannt wird:
 

Obwohl die Zustandssumme an dieser Stelle ganz unscheinbar eingeführt wurde, so hat sie doch eine gewaltige Bedeutung für die Spektroskopie, Statische Thermodynamik und die Reaktionsdynamik. Doch wir wollen den Ereignissen nicht vorgreifen.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.