Die Rotation - Energiewerte
![]()
Die Schrödingergleichung für zwei Teilchen, die sich in einem Potential
bewegen, dass nur vom Abstand r zwischen den Teilchen abhängt lautet
|
(− |
(1) |
wobei µ die reduzierte Masse der beiden Teilchen A und B, mA
und mB, darstellt: µ = mAmB/(mA+mB).
Wir wollen jetzt die möglichen Lösungen für y
und die dazugehörige Energie E suchen. Da es sich hier um ein kugelsymmetrisches Problem handelt, verwenden
wir zur Lösung der obigen Gleichung
Polarkoordinaten.
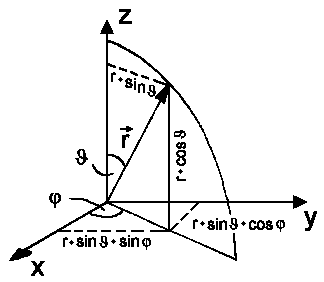 |
x = r sinJcosj
y = r sinJsinj
z = r cosJ
Vom Übergang zu den Polarkoordinaten ist in der Gleichung nur Δ betroffen, da das Potential V(r) schon in Polarkoordinaten angegeben ist:
Δ = ∂²/∂x² + ∂²/∂y² + ∂²/∂z²
= 1/r² ∂/∂r(r²
∂/∂r)
−1/r²h²L²
wobei der Operator L²(J,j) der Drehimpulsoperator zum Quadrat in Polarkoordinatendarstellung ist und nur von den Winkeln, nicht aber von r abhängt.
Bei einem zweiatomigen Molekül A-B, das um den gemeinsamen Schwerpunkt rotiert, verändert sich in dem von uns betrachteten idealisierten Fall die Bindungslänge nicht, d.h. die Atome sind wie mit einer festen Stange verbunden. Man spricht von einem starren Rotator. Die Radialkoordinate r ist also konstant, die entsprechenden Ableitungen verschwinden und V(r) können wir auf 0 festlegen. Wir erhalten danach die DGL:
1/2µr² L²Y = E Y
wobei wir statt der Wellenfunktion y nun Y schreiben, die nur von den Winkeln J,j abhängen kann. Führen wir noch das Trägheitsmoment I = µr² ein, dann gilt:
L² Y = 2I·E Y
Eine Lösung der DGL bezgl. der Winkelanteile entspricht daher einer
Bestimmung der Eigenfunktion des Drehimpulsoperators zum Quadrat. Die Größe
2I·E repräsentiert daher die Eigenwerte. Welche
Werte sind möglich? Eine
mathematische
Behandlung der Drehimpulseigenwerte zeigt, dass nur die Werte
l(l+1)h²
möglich sind, wobei l bei der Rotation nur die ganzzahligen
Werte l = 0,1,2,3,...annehmen kann:
| L² Y
= |
(2)
|
Für die Rotationsenergie erhalten wir also:
| E = |
E = B l(l+1) | l = 0,1,2,... |
wobei die Größe h²/2I
durch
B abgekürzt wurde. Im Allgemeinen wird B in Wellenzahlen [cm-1]
gemessen, so dass die Umrechnung gilt: B [cm-1] = h²/2Ihc
=
h/8π²cI
mit c als Lichtgeschwindigkeit.
![]()
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.