Optische Übergänge

Die Erzeugung von Licht durch optische Übergänge in Atomen (oder Molekülen) kann hier nicht detailliert quantenmechanisch dargestellt werden. In der für gewöhnlich ausreichenden Näherung kommen wir jedoch mit halbklassischen Rechnungen aus. In der klassischen Elektrodynamik sendet ein schwingender Dipol elektromagnetische Wellen aus. Der Dipol wird mathematisch durch das Dipolmoment
 

  = − e · (Ladung · Abstand [C · m])

beschrieben, wobei  der Vektor von der (+)Ladung zu der schwingenden (-)Ladung ist. Nach der "Übersetzungstabelle" klassische Größe quantenmechnischer Operator (→µ) müssen wir der Erwartungswert

<µ>  =  òy*() (− e) y() dV

für einen optischen Übergang berechnen.

[Ein Atom oder Molekül hat einen Durchmesser von einigen Angström; das Licht im sichtbaren Wellenlängenbereich von ca. 5000 Å. Aufgrund der größeren Ausdehnung der Welle ändert sich nicht die elektrische Feldstärke im räumlichen Bereich des Atoms oder Moleküls.]
 

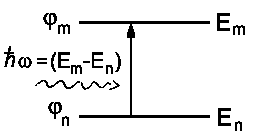Doch was sind die Wellenfunktionen y*, y ? Stellen wir uns ein Atom mit den beiden Energieniveaus En und Em und den entsprechenden Wellenfunktionen jn und jm vor. y() sei uns nun als Überlagerung dieser beiden Funktionen in der zeitabhängigen Form dargestellt:

y(,t)  =  1/Ö2[jn() e−iEnt/h + jm() e−iEmt/h]

(Da Licht elektromagnetische Strahlung ist, bei der das Feld schwingt, also sich zeitlich ändert, müssen wir die Zeit t "mitnehmen"; 1/Ö2 dient lediglich der Normierung).

Berechnung des Erwartungswertes <µmn(,t)>:
 

<µmn>  =  1/2 ∫(jn* eiEnt/h + jm* eiEmt/h)(−e)(jn e−iEnt/h + jm e−iEmt/h) dV
=  −e/2{ ∫jn* jn dV + òjm* jm dV +   òjn* jme−i(Em−En)t/h dV + òjm* jne+i(Em−En)t/hdV}
             |¾¾¾¾¾¾¾¯¾¾¾¾¾¾¾|
            zeitunabhängig		   |¾¾¾¾¾¾¾¾¾¾¾¾¯¾¾¾¾¾¾¾¾¾¾¾¾¾¾| 
zeitabhängig

Der zeitunabhängige Teil verschwindet sowohl für eine gerade als auch für eine ungerade Wellenfunktion j, denn |j|² ist gerade (|j()|²  =  |j(-)|²) und Multiplikation mit  sorgt dafür, dass die Integration über den ganzen Raum den Wert 0 (Null) ergibt.

Nutzen wir noch die Abkürzung w = (Em− En)/h, dann sehen wir, dass der Erwartungswert des Dipolmoments wie ein klassischer Dipol schwingt und damit das elektromagntische Feld erzeugt:
 

 <µmn> = ( −e òjm* .. jn dV eiwt   +  konjugiert komplex ) / 2

Wie wir weiter unten sehen werden, ist letztlich nur das Betragsquadrat |<µmn>|² für alle Bezüge zum Experiment relevant, so dass der konjugiert komplexe Teil genau den gleichen Beitrag wie der erste Teil der Formel liefert. Führen wir nun doch die Abkürzung

Rmn= òjm*  jm dV

ein, dann erhalten wir
 

<µmn> =  -e Rmn eiwt

Falls das obige Integral für Rmn verschwindet, dann ist der Übergang verboten (verbotener elektrischer Dipolübergang). Die Berechnung der Dipolmatrixelemente sind also von entscheidender Bedeutung bei der Berechnung optischer Übergänge.

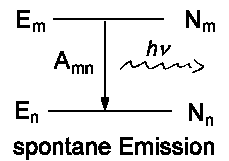
Ein Atom oder Molekül in einem angeregten Zustand der Energie Em geht in einen Zustand mit niedriger Energie En über, indem es spontan Licht emittiert. Ein Ensemble von angeregten Atomen (oder Molekülen) strahlt i.a. das Licht unabhängig voneinander ab. Die Strahlungsenergie Smn pro Zeit und Volumen für diese spontanen Übergänge ist dann:
 

Smn  =  Nm  hνmn Amn
Energieflußdichte / Jm-3s-1 ­ ­   ­ ­Übergangswahrscheinlichkeit für spontane Emission / s-1
  ·   Energiedifferenz Em− En ≡ Energie des Photons / J
 Dichte der Teilchen im angeregten Zustand / m-3

Es soll nun die Übergangswahrscheinlichkeit Amn [s-1] quantenmechnisch berechnet werden, indem wir eine Beziehung aus der Elektrodynamik auf die Quantenmechnik übertragen. Dort fand man für die Energieflußdichte S:

S  =  4/3. Nm/c³. 1/4peo. <|d²µ/dt²|²>t

wobei die Klammer <>t für den Zeitmittelwert einer zeitlich veränderlichen Größe (hier die 2. Ableitung des Dipolmoments nach der Zeit) steht. Der quantenmechanische Erwartungswert des Dipolmomentes ist <µmn> = −eRmneiwt, wovon wir nach 2-facher zeitlicher Ableitung den Quantenmittelwert bilden:

<|d²µ/dt²|²>t  =  |e Rmn w² eiwt|²  =  (2π)4νmn4 e² |Rmn|²

®      Smn  =   4/3. Nm/c³. 1/4peo· 16π4 νmn4 e² |Rmn|²


Smn  =  16π³/3. e²/eoc³. νmn4|Rmn|² · Nm
=  Nm hνmn Amn
Amn  =  8π²e²/3heoc³ . νmn³ |Rmn|²

Neben der spontanen Emission, die unabhängig von einem äußeren Strahlungsfeld ist und durch Amn charakterisiert wird, gibt es noch die induzierten Prozesse, die durch die Einwirkung von Licht auf das Teilchen hervorgerufen werden.
 

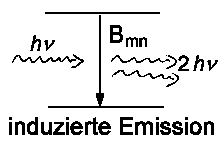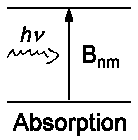
Die entsprechenden Koeffizienten Bnm für Absorption und Bmn für induzierte Emission sind bereits behandelt worden. Es gelten die Beziehungen:
 

Amn/Bmn  =  8πhν³/c³ und Bnm/Bmn  =  gm/gn

wobei gm- bzw. gn die Entartung der entsprechenden Energieniveaus angibt. Falls die Entartung gleich ist, dann gilt:
 

Bnm  =  Bmn

Die erste Gleichung stellt die wichtige ν³-Beziehung zwischen spontaner und induzierter Emission dar; die zweite Gleichung besagt, dass die Wahrscheinlichkeit für induzierte Emission gleich der für (induzierte) Absorption ist.
Mehr über Laser findet der Leser u.a. in "Spektrum der Wissenschaften": Anwendungen des Lasers, ISBN: 3-922508-47
Der Zusammenhang mit Rmn:

Bmn  =  e²/6eoh² |Rmn|²

 

Gelegentlich wird das Übergangsmoment durch die sogenannte Oszillatorstärke f ausgedrückt (dies kommt von der klassischen Betrachtungsweise, dass ein in drei Dimensionen frei schwingendes Elektron der Masse me die Oszillatorstärke f = 1 besitzt):
 

fmn  =  4p nmnme/3h |Rmn|²

Die Oszillatorstärke f ist dimensionslos. Intensive Übergänge erreichen typischerweise Oszillatorstärken zwischen 0,1 und 1, verbotene Übergänge liegen unterhalb von f ≈10-5.
 

Das Übergangsmoment µmn , sowie Rmn und fmn sind theoretische Größen; aber was messen wir im Experiment und wie kommen wir zu deb theoretischen Größen? Eine Antwort gibt's hier!



Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.