Raman-Spektren

Damit ein Übergang zwischen zwei nicht-entarteten Zuständen im Vibrations-Raman-Spektrum beobachtet werden kann, muss

G(y_v') xG(α_ij) xG(y_v'') = A

erfüllt sein. Mit α_ij sind die Komponenten des Polarisierbarkeitstensors α gemeint. Im allgemeinen sind die sechs Komponenten (α_xx, α_yy, α_xy, α_xz und α_yz) dieses Tensors verschieden. Diese Komponenten erscheinen in der rechten Spalte der Charaktertafel und sind auf diese Weise mit einer irreduziblen Darstellung verbunden. Bei Übergängen, bei denen mindestens ein Vibrationszustand entartet ist, muss die Gleichung entsprechend modifiziert werden:

G(y_v') xG(α_ij) xG(y_v'') É A

In vielen Fällen wird der untere Zustand der Schwingungsgrundzustand v = 0 sein, der vollkommen symmetrisch ist: G(y_v'') = A. Die Bedingungen für einen Raman-Übergang für nicht-entartete Schwingungen lautet damit:

G(y_v') = G(α_ij).

An Hand der Charaktertafel der Punktgruppe C_2v stellen wir fest, dass alle Grundschwingungen des H₂O im Raman-Spektrum erlaubt sind, denn es gilt G(α_xx, α_yy, α_zz) = A₁ und G(α_yz) = B₁. Entsprechend finden wir, dass alle Normalschwingungen des NH₃ (Punktgruppe C_3v) ebenfalls erlaubt sind, denn G( α_xx, α_yy, α_zz) = A₁ und G [(α_xx - α_yy, α_xy)(α_xx, α_yz)] = E.

In analoger Weise verfahren wir bei Acetylen, dessen Schwingungsmodi in untenstehender Tabelle zusammengefasst sind und das in Punktgruppe D_∞h fällt. Ein lineares Molekül mit N Atomen hat 3N-5 mögliche Normalschwingungen. Für Acetylen ergeben sich 7 Schwingungsmoden, wobei zu beachten ist, dass die beiden Biegeschwingungen jeweils zweifach entartet sind.

Normalschwingungen des Acetylens
	Mode	ν/cm^-1	irred. Darst.	infrarot- aktiv	Raman- aktiv
symmetrische CH-Streckschwingung	ν₁	3374	σ_g⁺	nein	ja
CC-Streckschwingung	ν₂	1974	σ_g⁺	nein	ja
antisymmetrische CH-Streckschwingung	ν₃	3287	σ_u⁺	ja	nein
trans-Biegeschwingung (zweifach entartet)	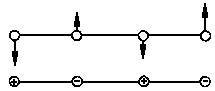ν₄	612	π_g	nein	ja
cis-Biegeschwingung (zweifach entartet)	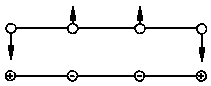ν₅	729	π_u	ja	nein

In der 1−0-Bande des Acetylens sind im Raman-Spektrum nur die Übergänge 1₀¹, 2₀¹ und 4₀¹ erlaubt. (In der verwendeten Notation bezeichnet die Zahl die Schwingung, die 2 beispielsweise die CC-Streckschwingung, der untere Index den ursprünglichen Schwingungszustand und der obere Index den Schwingungszustand nach Anregung).

Die Übergänge des Acetylens sind ein schönes Beispiel für das sogenannte Ausschlußprinzip. Liegt in einem Molekül ein Inversionszentrum vor, so sind die Grundschwingungen mit gerader Symmetrie (g-Schwingungen) Raman-aktiv, aber infrarot-inaktiv. Umgekehrt sind die infrarot-aktiven u-Schwingungen mit ungerader Symmetrie Raman-inaktiv. Kurz, die beiden Spektren schließen sich gegenseitig aus.

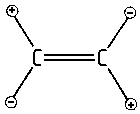Die ν₄π-Torsionsschwingung des Ethylens

Es gibt aber auch Schwingungsübergänge, die sowohl im Infrarot- als auch im Raman-Spektrum verboten sind. Ein Beispiel hierfür ist die nebenstehend dargestellte a_u-Torsionsschwingung des Ethylens. Die irreduzible Darstellung a_u weist in der Punktgruppe D_2h weder eine Translationskomponenten noch eine Komponente des Polarisierbarkeitstensors auf.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.