Rotational-vibrational spectra
The oscillating rotator
![]()
For a diatomic molecule, which we treat as a rigid rotator with a bond length fixed in the equilibrium position, the moment of inertia is Ie = µre2. Here, µ is the reduced mass.
In the case of a rotator in vibrational motion, re needs to be replaced by the average of the square of the the internuclear distance. Consequently, the moment of inertia becomes Iv = µ< r2>. Explicitly calculated with r = re ±s:
Iv = µ<r2> = µ<(re ± s)2> = µre2± 2<µsre> + µ<s2> = µre2 + µ<s2>
Within one oscillation, the addend 2<µsre> is compensated to zero. The third addend and the moment of inertia Iv remain for a molecule which has a vibration larger than µre2. In turn, the rotational constant B becomes dependent on the vibrational state. Note that Bv < Be
| with vibration: Bv = |
without vibration Be = |
Besides the approach from classical physics, the problem has as well been treated with purely mathematical means. A result of this is the following equation that represents a first approximation using a small correction coefficient αe to quantify the influence of the vibrational states v on the rotational constant Bv.
Bv = Be - αe(v + ½)
| Example HCl: αe = 0.3072 | ||||
| Be | Bv = 0 | Bv = 1 | Bv = 2 | Bv = 3 |
| 10.5934 cm-1 | 10.44 cm-1 | 10.13 cm-1 | 9.83 cm-1 | 9.52 cm-1 |
In addition to the influence of the molecule's oscillations, rotation itself affects molecular constants, i.e., centrifugation will stretch bonds (compare chapter Elastic rotor). The centrifugal stretching constant D introduces this phenomenon into our mathematical description of molecular energy levels. Note that, like B, constant D is function of the vibrational state and the correction coefficient βe quantifies the respective dependency.
Dv = De - βe(v + ½)
| Example HCl: βe = 7.51⋅10-6 | ||||
| De | Dv = 0 | Dv = 1 | Dv = 2 | Dv = 3 |
| 5.32⋅10-4 cm-1 | 5.28⋅10-4 cm-1 | 5.21⋅10-4 cm-1 | 5.13⋅10-4 cm-1 | 5.05⋅10-4 cm-1 |
First, we ignore the orientation of electron orbitals respective to the molecule's axis and expect the energies of rovibrational states to be the sum the following main ? addends.
| E = Evib + Erot = ωe(v + ½) - ωexe(v + ½)2 + BvJ(J + 1) - DvJ2(J + 1)2 |
We further ignore centrifugal stretching and keep on treating the possible
rotational states J as a parameter. Then, the energy differences for transitions
v' ← v with v' = v + 1 become:
| ΔE = | ωe -
2ωexe(v + 1) = ν0 |
+ {Bv'J'(J' + 1) - BvJ(J + 1)} |
For ΔJ = + 1 or J + 1 ← J, we speak of absorption peaks within the so-called R-branch. Their wavenumbers ν are
| ν = ν0 + 2Bv' + | (3Bv' - Bv)
> 0 |
J - | (Bv - Bv')
> 0 |
J2 | for J = 0, 1, 2, ... |
For ΔJ = - 1 or J - 1 ← J, we speak of absorption peaks within the so-called P-branch. Their wavenumbers ν are
| ν = ν0 - (Bv + Bv') J - (Bv - Bv') J2 for J = 1, 2, 3, ... |
The distance Δν between absorption line J and absorption line J+1 becomes
| R-branch: | Δ&nu = 2(2Bv' - Bv) - 2(Bv - Bv') J | distance decreases |
| P-branch: | Δν = 2Bv + 2(Bv - Bv')J | distance increases |
For Bv≈ Bv' , this distance is approximately 2B. The distance between the first transitions of the two branches is Δν ≈ 4Bv
Almost all diatomic molecules display such spectra with two branches R and P. As an example, hydrogen chloride is shown. Here, a natural mixture of isotopes served as a sample. Therefore, two species of HCl molecules with a relative difference of 0.15 percent in their reduced mass are present and some splitting occurs. The shift respective the wavenumbers of the lines of H35Cl and H37Cl is Δω ≈ 2cm-1.
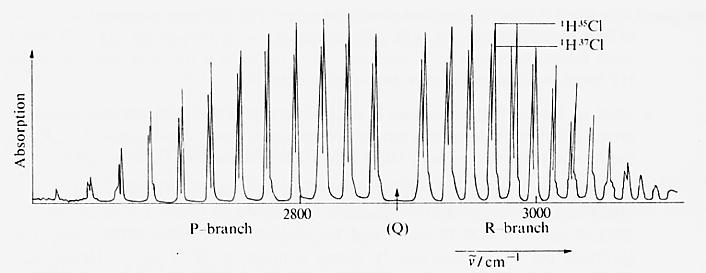 | ||
| vibrational levels Ev = (v + ½) hω0 |
rovibrational levels Er = B ⋅ J (J + 1) |
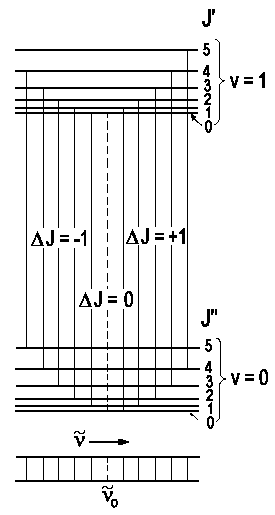 |
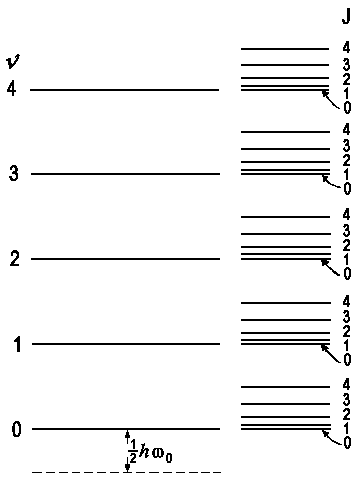 |
||
| P-branch
R-branch ΔJ = −1 ΔJ = +1 | ||
| Vibrational and rotational energy
levels of a diatomic molecule |
respective transitions | |
Some molecules display additional lines in the gap between the P- and the R-branch. These lines are connected to transitions with ΔJ = 0 and form the so-called Q-branch. As the rotation of the system is maintained, the axis of rotation must shift (ΔK ≠ 0) and a change of the angular momentum of electron orbitals must occur. If we consider diatomics, lines of a Q-branch must also have such an angular momentum which contributes to the total angular momentum of the molecule.
 |
| Projection of the electron's rotation onto the axis of
the molecule: Λ = 0, 1, 2, ... |
The quantum number Λ (recall chapter "Term
symbols and selection rules") denotes the projection of this orbital's
angular momentum onto the molecule's axis. For Λ = 0, nothing changes. For the
molecular total momentum, which includes rotation of nuclei and electrons, the
relation |J| ≥ |Λ| applies.
The respective energy levels are analogous to
those of the symmetric
top. Here, the constant A is in connection with the momentum of electron orbitals.
Note that A >> B.
| EJ = |
BJ (J + 1) due to rotation of nuclei |
+ |
(A - B) Λ2 due to electrons |
For Λ ≠ 0, there are new selection rules: Besides ΔJ = ±1, as well transitions with ΔJ = 0 are allowed.
With the NO molecule, we have this situation, but due to spin-related phenomenona, a detailed analysis is quite complicated. With no regard to the spin, there is the following approach to the lines of the Q-branch:
| E(v',J) - E(v,J) = ν0 + Bv' J(J+1) + (A-Bv')Λ2 - BvJ(J+1) - (A-Bv)Λ2 |
| ν = ν0 - (Bv-Bv')J(J+1) + (Bv-Bv')Λ2 |
As Bv ≈ Bv' , the lines within this branch lie very close to each other.
For the symmetric top, we have the following selection rules
| ΔK = 0 parallel band |
ΔJ = ±1 for K = 0 | diatomic molecules |
| ΔJ = 0, ±1 for K ≠ 0 | diatomic molecules, electronic contribution to J | |
| ΔK = ±1 perpendicular band |
ΔJ = 0, ±1 |
Of course, the intensity of rovibronic lines depends on the probability of a transition and on the occupancy of the involved states. In cases where ν = 0 is the only occupied vibrational level, the intensity of lines is proportional to the population NJ and the so-called Hönl-London-Factor SJ for this rotational state J.
| I ∝ NJ · |µJ'J|2 |
| I ∝ NJ · SJ |
As the transition probabilities for a simple rotator at high rotational states are in a quite narrow range, mainly the vibrational ground state distribution over J rules the intensity of lines. To find out the most probable rotational state, we fall back on Boltzmann's theory:
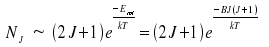
An estimation of the distribution is feasible if the distance betweeen the rotational levels is much smaller than the product kT, a condition which is fulfilled for temperatures around 300 Kelvin. We use dNJ/dJ = 0 as condition for a maximum.
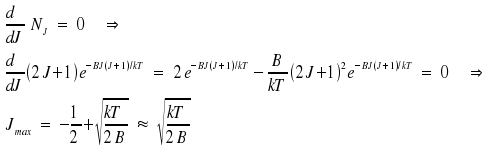
For Hydrogen chloride, we recieve a value around 2 or 3, for Hydrogen Iodide around 50. This approach paves the way to calculate temperatures, e.g. the temperature of the stratosphere, by using line intensities.
Chemical reactions often form products in abnormal state distributions. Provided the transistion probabilities, measurements of line intensities allow conclusions about such distributions. E.g., among the reactions that yield Hydrogene Fluoride, there are many where the HF molecules initially appear in some vibrationally excited state. Related techniques have been used by John C. Polanyi. In 1986, he, D.R. Herschbach and Y.T. Lee have been awarded with the nobel prize for their contributions to a more detailed understanding on reaction dynamics on the molecular level.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.