Comparison with the experiment

In chapter Optical Transitions, the theoretical quantities transition dipol moment µ_mn, matrix element R_mn, oszillator strength f_mn and Einstein's factors A_mn and B_mn for spontaneous and induced emission as well as B_nm for the phenomenon of absorption were presented. Now we aim on how to determine these quantities experimentally. First, we consider measurements where emission and absorption are resolved within time, then "ordinary" measurements of absorption. Treating emission like a first-order decay, the reduction of an initial number of excited species within time is

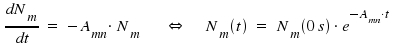
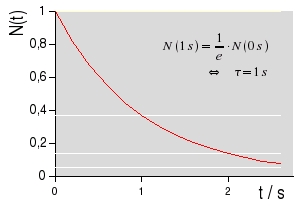Nm(0s)  is the initial number of particles within a certain volume and dNm / dt is the number of emitted photons per time. The life time τ of a state is defined as the time needed for a reduction by the factor of 1/e. Introducing τ yields the equation

Provided no processes like collisions with other particles or internal conversions occur, a measurment of the life time τ directly yields the transition probability A_mn. As the mentioned competitive processes reduce the life time, a higher transition probability is pretended. Having calculated A_mn, further theoretical quantities are within reach.

According to Lambert-Beer's law, light of an initial intensity I_o passes through a sample with an intensity I_trans when a beam travels along a path with length l where an absorbing substance is found. The concentration N this substance is here defined as the number of particles per volume. σ is introduced as the absorption coefficient for a defined wavelength.

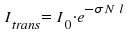
Adequate units are cm² for σ cm^-3 for N and cm for l. Using experimental data, we are now able to determine the absorption coefficient σ.

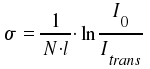
σ is dependent on the frequency ν. Through integration of σ over the frequencies &nu within an absorption peak, we obtain the total intensity for a transition n to m, which is connected with B_nm, the coefficient that reflects an atomic or molecular property.

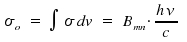
The obtained equation allows to estimate experimental values from an theoretical approach and, vice versa, to determine a transition coefficient B_nm by using experimental data. The above mentioned integration of σ over frequencies leads to the integrated absorption coefficient σ_o.

In laboratory practice, the extinction ε is the preferred measure to characterize the absorption of light by a substance. It is given in units of dm³ mol ^-1cm^-1 and defined as

We use the quotient I_trans/I₀ as a link between the two coefficients

As we introduced concentration N in molecules per volume and the unit of c is moles per volume, Avogadro's number N_A = 6.022·10²³mol^-1 appears.

N_A appears as well in the transformation factor between σ and ε. For this factor, we obtain

The conversion factor when using the conventional units dm³mol^-1cm-1 for ε and cm² for σ is 2,62 · 10²⁰. Further conversions between experimental quantities are found here. Due to integration over dν, the unit for frequency, Hertz or s^-1, becomes part of the unit of the integrated coefficients σ_o = ∫σdν resp. ∫εdν. Occasionally, integration is as well done over wavenumbers. Therefore, pay attention to the given units. Finally, an overview on the essential formulas:

All of the quantities are integrated and refer to a center frequency ν. In the next chapter, we will focus on the width of a line, i.e. σ(ν).

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.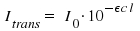
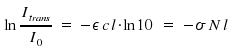
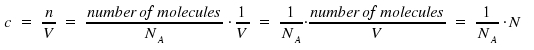
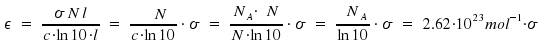
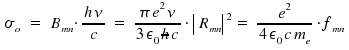
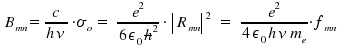
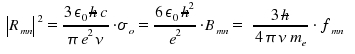
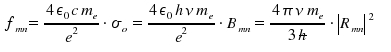