Optical Transitions

Here, it is not possible to describe the generation of light by optical transitions of atoms and molecules in detail. But a semiclassical mathematical treatment of the problem will yield a satisfying approximation. In classical electrodynamics, a dipol in vibration emits electromagnetic waves. It is defined by the dipol moment μ which is a vector defined as the product of separated charges of a magnitude Q and the vector r that represents the distance between the appearance of +Q and -Q. In our context, we express Q as a multiple of the electron's charge.

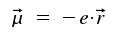With reference to the relation between classical quantities and quantum mechanical operators, we replace the vector μ by <μ> which denotes the expectation value for an optical transition.

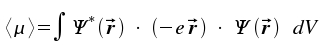An atom or a molecule has a diameter of several Ångström; whereas the wavelength of visible light is about 5000 Å. Therefore, the electric field appears to be constant within the dimensions of an atom or molecule. Now, let us focus on the wave functions Ψ* and Ψ. Imagine an atom with two energy levels E_n and E_m and the respective wave functions φ_n and φ_m.

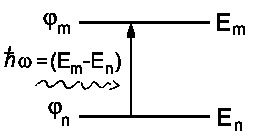Now we obtain Ψ(r) as a superposition of the time-dependent form of these two functions.

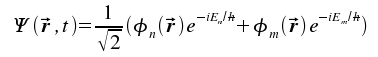As light is an electro-magnetic wave with field vectors changing in time, t appears in our mathematical treatment of the problem. The fraction 1/√2 normalizes the term. Now we are able to calculate the expectation value <μ> as a function of vector r and time t:

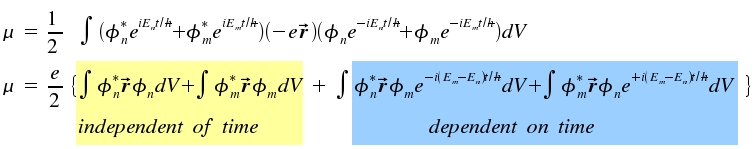
For gerade as well as for ungerade wave functions, |φ|² is even. Multiplication with vector r yields an integrand where the value for any volume element is compensated by the value for another volume element. Thus, the time-dependent addend disappears.

If we introduce ω = (E_m-E_n)/h, we recognize the same time dependencies for a classical dipol and for the quantum mechanical expectation value of μ. Thus, the latter produces an electromagnetic field.

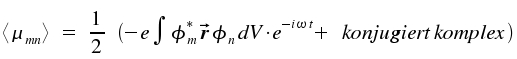As we will see below, only the square of the absolute value is of practical relevance. The contribution of the absolute value of the conjugated complex addend equals those of the first addend. We define R_mn for the integral

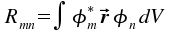and insert this abbreviation in our formula of the expectation value

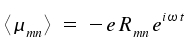The zeros of R_mn reflect forbidden transitions (forbidden electrical dipole transition). The calculation of the dipole matrix elements <μ_mn> is decisive for the treatment of optical transitions.

An atom or a molecule in an excited state of energy E_m changes to a state of lower energy E_n by emission of light. In general, a number of excited species radiates independently from each other. The energy S_mn per time and volume for spontaneous transitions is:

Now we want to calculate the transition probability A_mn [s^-1] in terms of quantum mechanics. We introduce an equation established in electrodynamics. The energy flux density S:

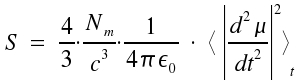Here, the brackets <>_t indicate the average value of a time dependent item (i.e. the second derivation of the dipol moment on time). The quantum mechanical expectation values for the dipole moment <μ_mn> = -eR_mne^iωt. Derivation of the term twofold on time and formation of the average yields:

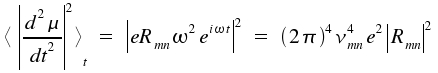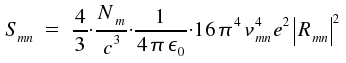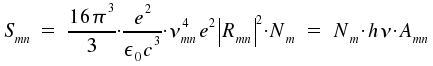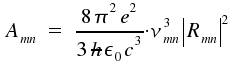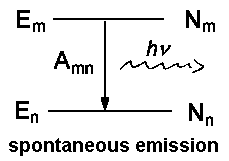
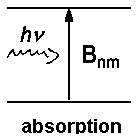
Besides spontaneous emission which is characterized by A_mn and occurs independently of an external field of radiation, there are as well processes introduced by the effects of light on the particle.

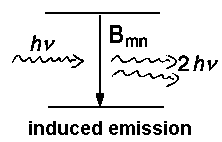In a previous lecture, we have already dealt with respective coefficients B_nm for absorption and B_mn for induced emission. The relation between the two coefficients is described by the following equations

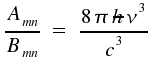and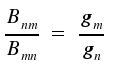

where g_m- and g_n represent the degeneracy of the respective energy levels m and n. For identical degeneracy of both levels, we have

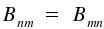The first equation establishes the important ν³-relation between spontaneous and induced emission. The second equation states identical probabilities for induced emission and (induced) absorption. The described processes are fundamental for lasers . The coeffient for induced emission B_mn is proportional the integral for which we use the abbreviation R_mn.

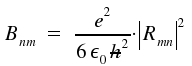Occasionally, the transition dipol moment <μ> is replaced by the oscillator strength f. In a classical approach, where we deal with oscillations of a charged species, this dimensionless quantity has the value f = 1 for an electron which is characterized by charge -e and mass m_e. The following equation allows to calculate the oscillator strength for molecular transitions using R and frequency ν For intense transitions f varies between 0.1 and 1 whereas forbidden transitions has magnitudes of 10^-5.

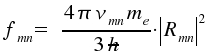Transition dipole moment µ_mn, R_mn and oscillator strength _mn are terms in a theory of molecular transitions. In an extra chapter, we will focus on quantities that can be measured and will pave the way from experiments to the the approach presented here.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.