


Next: CI mit Ein- und
Up: CI- und Coupled-Cluster-Methoden
Previous: Limited CI
Die Slater-Determinanten, die man aus einer festen Orbitalbasis
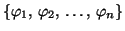 bilden kann, lassen
sich im geschlossenschaligen Fall danach klassifizieren, je nachdem wieviele
(``besetzte'') Orbitale in der Hartree-Fock-Determinanten
bilden kann, lassen
sich im geschlossenschaligen Fall danach klassifizieren, je nachdem wieviele
(``besetzte'') Orbitale in der Hartree-Fock-Determinanten 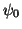
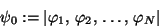 |
(87) |
durch dort unbesetzte, ``virtuelle'' ersetzt worden sind.
Man kann nun sogenannte ``angeregte'' oder ``substituierte'' Determinanten
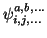 definieren, bei denen die in
definieren, bei denen die in 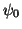 vorhandenen (``besetzten'')
Orbitalen (mit den Indizes
vorhandenen (``besetzten'')
Orbitalen (mit den Indizes
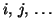 )
durch dort nicht vorhandene
(``unbesetzte,'' ``virtuelle'') Orbitale (mit den Indizes
)
durch dort nicht vorhandene
(``unbesetzte,'' ``virtuelle'') Orbitale (mit den Indizes
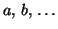 )
ersetzt worden sind.
Je nachdem, wieviele Orbitale ersetzt wurden, unterscheidet man:
)
ersetzt worden sind.
Je nachdem, wieviele Orbitale ersetzt wurden, unterscheidet man:
- Einfachersetzungen (``Singles,'' S):
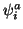
- Zweifachersetzungen (``Doubles,'' D):
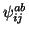
- Dreifachersetzungen (``Triples,'' T):
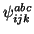
- Vierfachersetzungen (``Quadruples,'' Q):
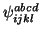
- usw.
Man kann nun die Wellenfunktion 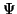 entsprechend aufteilen
entsprechend aufteilen
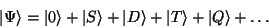 |
(88) |
in die Schrödinger-Gleichung (26)
einsetzen
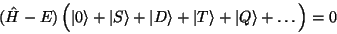 |
(89) |
und schließlich nacheinander von links mit
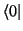 ,
,
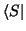 ,
,
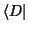 ,
usw. projizieren.
Man erhält dann unter Berücksichtigung der Tatsache, daß
,
usw. projizieren.
Man erhält dann unter Berücksichtigung der Tatsache, daß 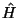 nur
maximal Zweiteilchenoperatoren enthält, folgende Gleichungen:
nur
maximal Zweiteilchenoperatoren enthält, folgende Gleichungen:
usw.
Die Gln. (90) kann man nun umformen zu
Das heißt, die Gesamtenergie E und damit auch die
Korrelationsenergie Ec, läßt sich allein aus der Kenntnis der
Wellenfunktion bis hin zu den Doppeltersetzungen berechnen.
Allerdings ist zur Berechnung dieses Anteils der Wellenfunktion natürlich
die Berücksichtigung der höheren Anteile, also
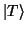 ,
,
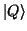 ,
usw. erforderlich.
,
usw. erforderlich.
Aus dieser sogenannten ``Nesbet-Hierarchie'' könnte man schlußfolgern,
daß die Ein- und Zweifach-Ersetzungen den wichtigsten Teil der
CI-Wellenfunktion ausmachen.
In der Tat erhält man mit diesem sogenannten CI(SD), siehe nächsten
Abschnitt, in gutmütigen Fällen bereits ca. 95 % der Korrelationsenergie.



Next: CI mit Ein- und
Up: CI- und Coupled-Cluster-Methoden
Previous: Limited CI
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.