| |
(103) |
Im Gegensatz zu den oben beschriebenen CEPA-Methoden, können die sog. Coupled-Cluster (CC)-Methoden [18]
streng size-extensive formuliert werden.
Die CC-Methoden basieren auf dem Ansatz von Coester und Kümmel
[19,20,21]
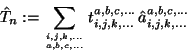 |
(105) |
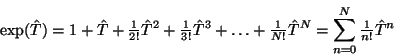 |
(106) |
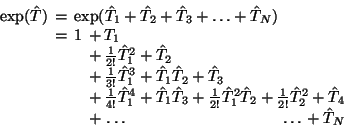 |
(107) |
Der Anregungsoperator ![]() kann nun z.B. auf Ein- und
Zweifachersetzungen,
kann nun z.B. auf Ein- und
Zweifachersetzungen, ![]() und
und ![]() (d.i. CC(SD))
beschränkt werden, ohne daß die Eigenschaft der Size-Extensivity verloren geht.
Denn man erhält in diesem Fall
(d.i. CC(SD))
beschränkt werden, ohne daß die Eigenschaft der Size-Extensivity verloren geht.
Denn man erhält in diesem Fall
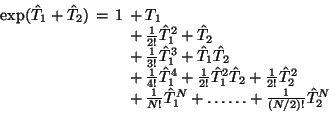 |
(108) |
Inzwischen existieren auch für allgemeine offenschalige Fälle effiziente CC(SD)-Implementierungen mit ähnlichen Rechenzeiten wie für CEPA. Die Erweiterung des CC(SD) auf Dreifach-Ersetzungen (engl. ``triples'') [23,24], die meist näherungsweise berücksichtigt werden [25,26,27], liefert in vielen Fällen Ergebnisse, die in der Genauigkeit z.B. MR-CI(SD) in nichts nachstehen.
Eine Methode, die die Flexibilität von MR-CI(SD) mit der Eigenschaft der exakten Size-Extensivity vereinigt, ist das MR-CC(SD) [28]. Leider sind jedoch, aufgrund von verschiedenen Schwierigkeiten, (dies sind insbesondere Schwierigkeiten, die mit dem Auftreten der, schon von störungstheoretischen Rechnungen auf MR-Niveau her bekannten, sog. Intruder-Zuständen verbunden sind) bislang keine konkurrenzfähige Anwendungen gelungen. Aus diesem Grund ist man derzeit, zum Erzielen größtmöglicher Genauigkeit, bei der näherungsweisen Lösung der elektronischen Schrödinger-Gleichung von Mehrelektronensystemen, nachwievor auf die Verwendung von MR-CI(SD) bzw. MR-ACPF angewiesen.
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.