


Next: Das Coupled-Cluster (CC) -Verfahren
Up: CI- und Coupled-Cluster-Methoden
Previous: Das Size-Extensivity-Problem
Wir wollen nun das Problem der Size-Extensivity mathematisch analysieren und
durch einen Trick beheben.
Zu diesem Zweck definieren wir nach Löwdin die sogenannte
Korrelationsenergie Ec
wobei E0 die Hartree-Fock-Energie ist.
Die CI(D)-Wellenfunktion 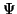 teilen wir gleichermaßen auf
teilen wir gleichermaßen auf
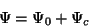 |
(97) |
wobei 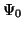 die Hartree-Fock-Wellenfunktion ist und
die Hartree-Fock-Wellenfunktion ist und 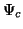 alle
Doppeltersetzungen aus
alle
Doppeltersetzungen aus 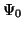 enthält.
enthält.
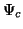 ist automatisch orthogonal zu
ist automatisch orthogonal zu 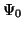 .
der Einfachheit halber soll nicht
.
der Einfachheit halber soll nicht 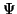 selbst, sondern nur der Anteil
selbst, sondern nur der Anteil
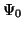 auf eins normiert sein, d.h.
auf eins normiert sein, d.h.
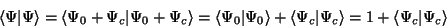 |
(98) |
Diese Art der Normierung nennt man ``intermediär.''
Der entsprechend modifizierte Rayleigh-Quotient (vgl. Gln. [27]) ist
gegeben durch
![\begin{displaymath}
F_c[\Psi_c] := {\langle\Psi_0+\Psi_c\vert\hat H-E_0\vert\Psi_0+\Psi_c\rangle \over
1 + \langle\Psi_c\vert\Psi_c\rangle}
\end{displaymath}](img214.gif) |
(99) |
Wir wollen nun dieses Funktional gemäß der Methode der
Variationsrechnung (siehe Abschnitt 2.1) stationarisieren.
Wir suchen also eine feste Funktion 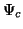 ,
die bei beliebigen
Variationen
,
die bei beliebigen
Variationen
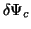 ,
die jedoch orthogonal zu
,
die jedoch orthogonal zu 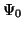 sein sollen,
das Funktional F stationarisiert, d.h.
sein sollen,
das Funktional F stationarisiert, d.h.
![\begin{displaymath}\delta_1 F[\Psi_c+\Psi_c] \stackrel{!}{=} 0
\end{displaymath}](img216.gif) |
(100) |
Man kann sich überlegen, daß die Bedingung dafür, gegeben ist durch die
Gleichung
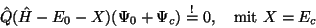 |
(101) |
mit dem Projektionsoperator
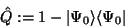 |
(102) |
der die Anteile von 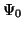 herausprojiziert.
Man erkennt nun (mit etwas Übung) unmittelbar, daß die zu lösende Gleichung
(101) nicht size-extensiv sein kann.
Der Grund liegt im Shift X von
herausprojiziert.
Man erkennt nun (mit etwas Übung) unmittelbar, daß die zu lösende Gleichung
(101) nicht size-extensiv sein kann.
Der Grund liegt im Shift X von 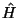 ,
der ja im Falle separierter Systeme,
von der Korrelationsenergie des Gesamtsystems abhängt, obgleich
,
der ja im Falle separierter Systeme,
von der Korrelationsenergie des Gesamtsystems abhängt, obgleich 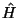 blockdiagonal ist und
blockdiagonal ist und 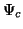 gegeben ist als direkte Summe.
gegeben ist als direkte Summe.
Die Idee der ``Coupled Electron-Pair Approximation'' (CEPA) ist, in Gln. (99)
den Shift X so zu modifizieren, daß er unabhängig von der
Größe des Gesamtsystems ist.
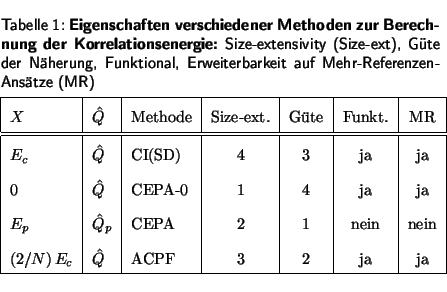
Von Interesse sind insbesondere die in Tabelle
1 aufgeführten Möglichkeiten.
In der ersten Zeile ist das bereits beschriebene CI(SD) mit den
bekannten Mängeln aufgeführt.
Läßt man den Shift ganz weg, so erhält man das streng
size-extensive CEPA-0, das die Korrelationsenergie
leider so sehr überschätzt, daß es für praktische
Anwendungen nicht in Frage kommt.
Spaltet man die Korrelationsenergie in Beiträge auf, die von
einzelnen Paaren herrühren, und shiftet jedes Diagonalelement
von
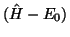 mit der entsprechenden sog. Paarkorrelationsenergie,
so gelangt man zum CEPA von Kelly und Meyer.
Benutzt man einen entsprechend gemittelten Shift, so gelangt man
zum ``Averaged Coupled-Pair Functional'' (ACPF)
[17], das sich auch auf den Mehrreferenzenfall
erweitern läßt.
mit der entsprechenden sog. Paarkorrelationsenergie,
so gelangt man zum CEPA von Kelly und Meyer.
Benutzt man einen entsprechend gemittelten Shift, so gelangt man
zum ``Averaged Coupled-Pair Functional'' (ACPF)
[17], das sich auch auf den Mehrreferenzenfall
erweitern läßt.



Next: Das Coupled-Cluster (CC) -Verfahren
Up: CI- und Coupled-Cluster-Methoden
Previous: Das Size-Extensivity-Problem
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() mit der entsprechenden sog. Paarkorrelationsenergie,
so gelangt man zum CEPA von Kelly und Meyer.
Benutzt man einen entsprechend gemittelten Shift, so gelangt man
zum ``Averaged Coupled-Pair Functional'' (ACPF)
[17], das sich auch auf den Mehrreferenzenfall
erweitern läßt.
mit der entsprechenden sog. Paarkorrelationsenergie,
so gelangt man zum CEPA von Kelly und Meyer.
Benutzt man einen entsprechend gemittelten Shift, so gelangt man
zum ``Averaged Coupled-Pair Functional'' (ACPF)
[17], das sich auch auf den Mehrreferenzenfall
erweitern läßt.