Fein, Hyperfein und der Drehimpuls des Photons

Zeeman Effekt
Wir wollen nun den Einfluss einer Bewegung des Elektrons um einen positiven
Kern näher betrachten. In Niels Bohr's klassischer Beschreibung bewegt
sich das Elektron auf einer geschlossenen Bahn. Damit verbunden ist ein
Ringstrom I = −e/τ
(τ: Umlaufzeit). Mit einem solchen Strom ist
ein magnetisches Moment 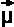 verknüpft, das über µ = I · F gegeben
ist. Mit F = π r² (Fläche die überstrichen
wird) erhalten wir µ = I · F = −e/τ
(π r²). Für den Drehimpuls gilt L
= mevr = me2pr²/τ
, da v=2πr/τ
verknüpft, das über µ = I · F gegeben
ist. Mit F = π r² (Fläche die überstrichen
wird) erhalten wir µ = I · F = −e/τ
(π r²). Für den Drehimpuls gilt L
= mevr = me2pr²/τ
, da v=2πr/τ
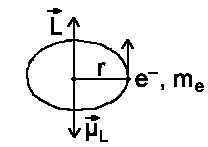 Wir erhalten danach:
Wir erhalten danach:
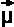 L
= − e/2me L
= − e/2me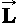 |
Da in der Quantenmechanik der Drehimpuls durch einen Operator dargestellt
wird, erhalten wir für die Eigenwerte µLz einer z-Komponente
(Lz y
= ml h y):
µLz = −
e/2meh·
ml mit der Abkürzung
µB = eh/2me
(Bohrsches Magneton)
µLz = −µB·
ml mit µB
= eh/2me |
µB = eh/2me
= 9,273 · 10-24 Am² = 9,273
·
10-24 J/T = 5,787
.
10-5 eV/T
= 0,4668 cm-1/T = 1,4 · 1010Hz/T
(T: Tesla)
Die Energie eines solchen Systems im Magnetfeld der Stärke 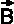 ist danach
ist danach
| EB = −µLz·
B = µB · ml·
B |
und die Gesamtenergie ist E = E0 + EB, d.h.
die Energieniveaus mit dem Drehimpuls zur Quantenzahl l spalten
in 2l + 1 Niveaus auf:
 |
Dieser Effekt wird
als normaler Zeeman-Effekt bezeichnet |
Der Grundzustand des Wasserstoffs sollte danach (ml
= 0) nicht beeinflusst werden. Dies ist nicht der Fall, da H paramagnetisch
ist! Die Ursache ist der Elektronenspin. Man mag nun vermuten,
dass für den Spin das gleiche gilt, wenn man die klassische Vorstellung
eines um die eigene Achse sich drehenden Elektrons als Ursache für
den Spin annimmt. Doch findet man hier
µSz = −gS
µB · ms
EB = gS· µB·
ms· B |
Der so genannte gyromagnetische Faktor gS ergibt sich
aus der relativistischen Dirac-Gleichung
zu gS = 2. Das Experiment liefert
gS = 2,00231930438(6)
Dieser Wert wird von der Quantenelektrodynamik erklärt,
die eine vollständige Quantentheorie des elektromagnetischen Feldes
ist. Dabei wird das elektromagnetische Feld in Normalschwingungen zerlegt,
die wie beim harmonischen Oszillator quantisiert werden. Dabei kommt jeder
Normalschwingung die Nullpunktsenergie hw/2
zu. Das bedeutet, dass fluktuierende elektromagnetische Felder vorhanden
sind, auch wenn keine äußeren Felder einwirken. Obwohl die mittleren
Feldstärken verschwinden, sind die quadratischen Mittelwerte
der Felder ungleich Null, was zu mittleren quadratischen Schwankungen der
Ortskoordinate führt.
Näheres zum Zeeman-Effekt findet man hier.
Die Größe gS · µB≈
28 GHz/T gibt an, wie groß
der Energieabstand aufgrund des Elektronenspins durch Anlegen eines Magnetfeldes
ist. Da die heute erzeugbaren Magnetfelder bei einigen Tesla liegen, erwarten
wir Übergänge im Gigahertzbereich (Mikrowellen) beim Anlegen
solcher Felder. Bei der Elektronen-Spin-Resonanz (ESR)-Spektroskopie
muss man daher mit Mikrowellen arbeiten. Bei der NMR
sind es Radiowellen im MHz-Bereich. Den sehr einfachen Grund finden wir
später.
Die Spin-Bahn-Kopplung
Die zwei Orientierungsmöglichkeiten des Elektronenspins (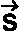 )
relativ zum Bahndrehimpuls (
)
relativ zum Bahndrehimpuls (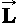 )
bewirken eine Verdopplung der Energieniveaus (natürlich außer
s-Niveaus), die spektroskopisch beobachtbar ist, da die Spektrallinie bei
genügend hoher Auflösung als Linienpaar (Dublett) sichtbar wird.
Das bekannteste Beispiel hierfür ist die Natrium D-Linie bei den Wellenlängen
5890 Å und 5896 Å. Zum Verständnis der Spin-Bahn-Kopplung
(oder Wechselwirkung) "setzen" wir uns in Gedanken zunächst auf den
Atomkern: Das Elektron "umkreist" uns (resp. den Kern) mit dem Bahndrehimpuls
)
bewirken eine Verdopplung der Energieniveaus (natürlich außer
s-Niveaus), die spektroskopisch beobachtbar ist, da die Spektrallinie bei
genügend hoher Auflösung als Linienpaar (Dublett) sichtbar wird.
Das bekannteste Beispiel hierfür ist die Natrium D-Linie bei den Wellenlängen
5890 Å und 5896 Å. Zum Verständnis der Spin-Bahn-Kopplung
(oder Wechselwirkung) "setzen" wir uns in Gedanken zunächst auf den
Atomkern: Das Elektron "umkreist" uns (resp. den Kern) mit dem Bahndrehimpuls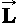 .
Setzen wir uns auf das Elektron, dann umkreist uns der Kern und erzeugt
ein magnetisches Feld
.
Setzen wir uns auf das Elektron, dann umkreist uns der Kern und erzeugt
ein magnetisches Feld 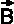 ,
das parallel zu
,
das parallel zu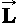 steht (wegen
der positive Ladung des Kerns). Da das Elektron (auf dem wir in Gedanken
sitzen) ruht, gibt es nun eine Wechselwirkung des magnetischen Feldes mit
dem magnetischen Moment
steht (wegen
der positive Ladung des Kerns). Da das Elektron (auf dem wir in Gedanken
sitzen) ruht, gibt es nun eine Wechselwirkung des magnetischen Feldes mit
dem magnetischen Moment 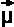 S
des Spins. Die Wechselwirkung ist proportional zu
S
des Spins. Die Wechselwirkung ist proportional zu 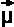 S.
S.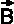 .
Da
.
Da 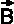 ||
||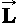 und
und 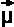 S ||
S ||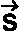 ist die Wechselwirkung proportional zu
ist die Wechselwirkung proportional zu 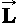 .
.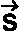 ,
was den Namen Spin-Bahn-Kopplung erklärt. Die Energie des Elektrons
aufgrund dieser Wechselwirkung ist dann
,
was den Namen Spin-Bahn-Kopplung erklärt. Die Energie des Elektrons
aufgrund dieser Wechselwirkung ist dann
ESL = cSL.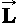 .
.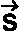 /
/h²
wobei die Proportionalitätskonstante cSL über die
Dirac'sche Gleichung berechnet werden kann.
Was ist mit 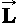 .
.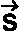 ? Nun, wir
haben als Messgröße (oder Observable) den Gesamtdrehimpuls
? Nun, wir
haben als Messgröße (oder Observable) den Gesamtdrehimpuls 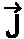 :
:
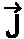 =
= 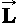 +
+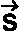 Natürlich können wir in der Quantenmechanik nicht den Vektor,
d.h. alle drei Komponenten, exakt festlegen, wohl aber den Betrag und eine
Komponente! Quadrieren der obigen Gleichung ergibt:
J² = L² + S² + 2
Natürlich können wir in der Quantenmechanik nicht den Vektor,
d.h. alle drei Komponenten, exakt festlegen, wohl aber den Betrag und eine
Komponente! Quadrieren der obigen Gleichung ergibt:
J² = L² + S² + 2 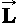 .
.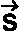 ®
® 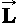 .
.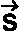 =
½ (J² − L² −
S²)
Da die Quadrate der Drehimpulse Erhaltungsgrößen sind, können
wir die quantenmechanischen Operatoren durch die Eigenwerte ersetzen (wir
benutzen nun Großbuchstaben für die Eigenwerte, da die Aussagen
nicht nur fürs H-Atom gelten):
=
½ (J² − L² −
S²)
Da die Quadrate der Drehimpulse Erhaltungsgrößen sind, können
wir die quantenmechanischen Operatoren durch die Eigenwerte ersetzen (wir
benutzen nun Großbuchstaben für die Eigenwerte, da die Aussagen
nicht nur fürs H-Atom gelten):
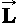 .
.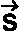 º
L.
S
= ½ [J(J + 1) −
L(L + 1) − S(S + 1)]
º
L.
S
= ½ [J(J + 1) −
L(L + 1) − S(S + 1)] h²
Wir erhalten danach für die Spin-Bahn-Kopplungsenergie:
ESL = cSL/2[J(J
+ 1) − L(L + 1) −
S(S + 1)]
Die Größe cSL ist durch Ausmessen der Dublettstruktur
in den optischen Spektren direkt messbar.
Beim H-Atom erhalten wir (J = L ± S, S = ½)
ESL ( ≡
J = L + ½) = ½ cSL ·
L
ESL (¯ ≡
J = L − ½) = −
½ cSL (L + 1)
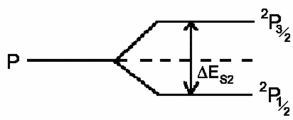 |
J = L + S ≡
1 + ½ = 3/2 |
| J = L − S ≡
1 − ½ = ½ |
Die Separation zwischen den Niveaus ist
ΔESL = ESL()
−
ESL (¯) = ½
cSL (2L + 1)
 Zusammen mit der Proportionalitätskonstante cSL erhält
Dirac
für die Energieaufspaltung der Spin-Bahn-Wechselwirkung:
ΔESL = |En|
Z²α²/n
l(l
+1) ≈ 5,3 ·
10-5 Z²/n
l(l
+ 1) |En|
mit α = e²/4π
Zusammen mit der Proportionalitätskonstante cSL erhält
Dirac
für die Energieaufspaltung der Spin-Bahn-Wechselwirkung:
ΔESL = |En|
Z²α²/n
l(l
+1) ≈ 5,3 ·
10-5 Z²/n
l(l
+ 1) |En|
mit α = e²/4πh²ε0c
= 1/137,0359895, die nach Sommerfeld
benannte Feinstrukturkonstante. Die Energieeigenwerte für das komplette
Wasserstoffatom (Spin-Bahn + Relativ. Effekt) ergeben sich nach der Dirac'schen
Theorie zu:
EnJ = − mc²/2α²Z²/n²{1
+ α²Z²/n(1/J
+ ½− ¾ n)}
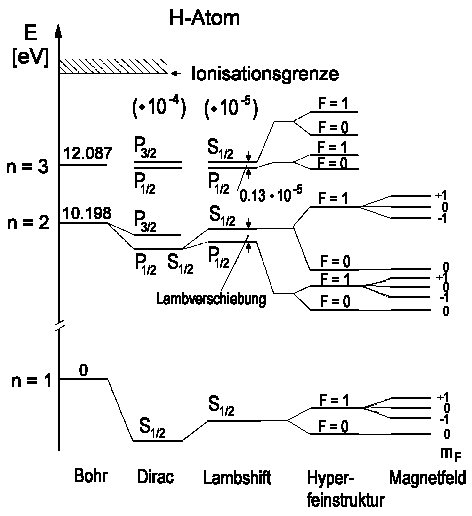
Nach dieser Theorie sind die Energieniveaus mit gleichen J und n entartet.
Z.B. sollten die Zustände 2²S½ und 2²P½
die gleiche Energie haben. Lamb und Rutherford
gelang jedoch 1947 der Nachweis, dass diese Entartung nicht den experimentellen
Tatsachen entspricht. Sie konnten mit Hilfe der Hochfrequenzspektroskopie
den Übergang ²S½ ←
²P½ anregen, d.h. die Energieniveaus sind aufgespaltet,
also nicht entartet; allerdings beträgt die Aufspaltung nur
0,03528 cm-1.
Doch damit noch nicht genug: Es gibt noch eine weitere Aufspaltung
der Spektrallinien; die so genannte Hyperfeinstruktur. Diese
wird durch die Wechselwirkung des Magnetfeldes (aufgrund der Elektronenbewegung)
mit dem Kernspin hervorgerufen. Der Kern des Wasserstoffatoms, also das
Proton, besitzt wie das Elektron den Spin I = ½ und damit ein magnetisches
Moment 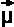 P
= −gI e
P
= −gI eh/2mp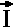 /
/h
= µK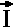 /
/h
Aufgrund der hohen Masse mp ist µK ≡
Kernmagneton (µK = gI eh/2mp)
um den Faktor me/mp
kleiner !
Analog zur Feinstrukturkopplung müssen wir nun 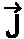 und
und 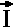 koppeln, woraus der
"neue" Gesamtdrehimpuls entsteht:
koppeln, woraus der
"neue" Gesamtdrehimpuls entsteht:
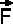 =
= 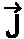 +
+ 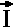 mit Fy
= F(F +1)
mit Fy
= F(F +1) h² y und
Fzy
= mF hy
; mF = −F,
−F+1,
... F−1, F
Quadrieren der Gleichung für 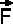 und Auflösen nach
und Auflösen nach 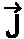 .
.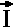 liefert analog
zum Ausdruck für die Feinstruktur die Erwartungswerte für die
Hyperfeinenergie:
liefert analog
zum Ausdruck für die Feinstruktur die Erwartungswerte für die
Hyperfeinenergie:
EHFS = cHFS/2{F(F
+ 1) - J(J + 1) - I(I + 1)}
Der niedrigste Term bei Wasserstoff 1²S½
spaltet danach in die beiden Terme mit F = 1 (Spin Elektron und Spin Proton
)
und F = 0 (Spin Elektron und Spin Proton ¯
antiparallel) auf. Ein Übergang zwischen diesen beiden Niveaus kann
nur stattfinden, wenn der Spin umklappt. Dies ist extrem unwahrscheinlich
(in der Tat beträgt die hierfür benötigte Zeit beim H-Atom
ungefähr 10 Millionen Jahre), doch wird auch dieser Übergang
im Weltall beobachtet (keine Stöße, viel H). Er liegt bei n»
1,4204 GHz (λ = 21 cm).
Da dieser Übergang den Drehimpuls des Systems von F = 1h
nach F = 0h überführt, andererseits aber
der Gesamtdrehimpuls in jedem Fall erhalten bleiben muss, folgt
daraus, dass das Photon den Drehimpuls des Wasserstoffatoms übernommen
haben muss. Also besitzt auch das Photon einen Drehimpuls.
Dieser Spin des Photons beträgt aber
Genau genommen ist die Bezeichnung Spin des Photons nicht
sehr glücklich gewählt, da eine Projektion des "Photonenspins"
auf die Flugachse nur die Werte m = +1 oder m = -1 liefert, entsprechend
rechts- und linkszirkular polarisiertem Licht, aber niemals m=0, was einer
longitudinalen Polarisation des Lichtes entsprechen würde, die es
aber nicht gibt!
Der Spin des Photons hat bedeutsame Folgen für optische Spektren,
denn wir erhalten Auswahlregeln für die Übergänge.
Für einen Übergang zwischen dem initialen Niveau i und dem finalen
f mit den Drehimpulsen 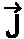 i
bzw.
i
bzw.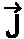 f muss
aufgrund der Drehimpulserhaltung gelten:
f muss
aufgrund der Drehimpulserhaltung gelten:
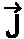 i
=
i
= 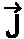 f +
f + 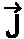 Photon
Natürlich muss
Photon
Natürlich muss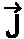 Photon
nicht zwangsläufig gleich
Photon
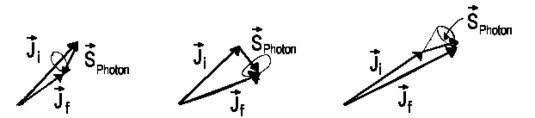
nicht zwangsläufig gleich 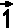 sein, denn prinzipiell kann das Photon neben dem Spin noch relativ zum
Atom einen Bahndrehimpuls besitzen. Anschaulich bedeutet die Emission eines
Photons mit nichtverschwindenden Bahndrehimpuls, dass das Photon aus den
Randregionen emittiert wird. Dieser Prozess ist jedoch äußerst
unwahrscheinlich, so dass für die Quantenzahlen Ji und
Jf aufgrund der Drehimpulserhaltung die Beziehung
gelten muss.
sein, denn prinzipiell kann das Photon neben dem Spin noch relativ zum
Atom einen Bahndrehimpuls besitzen. Anschaulich bedeutet die Emission eines
Photons mit nichtverschwindenden Bahndrehimpuls, dass das Photon aus den
Randregionen emittiert wird. Dieser Prozess ist jedoch äußerst
unwahrscheinlich, so dass für die Quantenzahlen Ji und
Jf aufgrund der Drehimpulserhaltung die Beziehung
gelten muss.
 |
ΔJ = −1
ΔM = 0 , ±1
P-Zweig |
ΔJ = 0
ΔM = ±1
Q-Zweig |
ΔJ = +1
ΔM = 0 , ±1
R-Zweig |
Falls Jf = 0 und Ji = 0 sind, dann ist ΔJ=0
wegen der Drehimpulserhaltung immer streng verboten. Wenn die Wechselwirkung
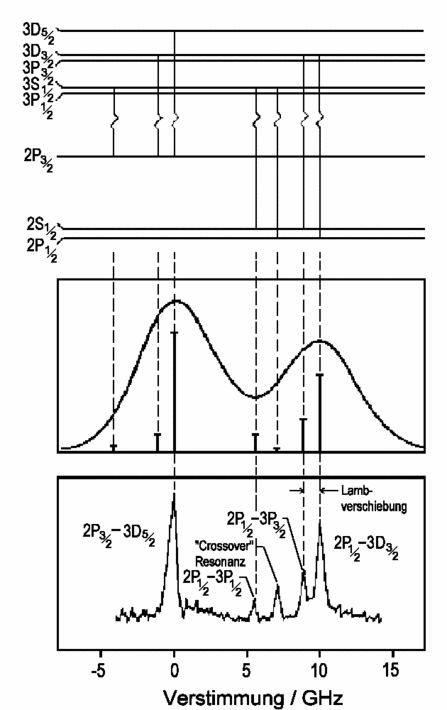
zwischen  und
und 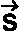 vernachlässigbar klein ist, dann "mag der Spin nicht umklappen" und
es gilt die weitere (nicht ganz so zwingende) Auswahlregel:
vernachlässigbar klein ist, dann "mag der Spin nicht umklappen" und
es gilt die weitere (nicht ganz so zwingende) Auswahlregel:
 Die Auswahlregel für den Elektronenbahndrehimpuls sei hier schon einmal
ohne Ableitung angegeben:
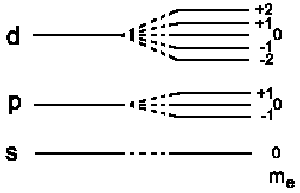
Die möglichen Übergänge sind in der Abbildung angegeben
(Balmer a-Linie, n = 3 ↔
n = 2). Die aufgrund der Bewegung der H-Atome verbreiterten Linien (Doppler-Verbreiterung)
können mit Hilfe der Dopplerfreien Spektroskopie aufgelöst werden
und die exakte Vermessung der Linienabstände erlaubt eine detaillierte
Überprüfung der Theorie.
Die Auswahlregel für den Elektronenbahndrehimpuls sei hier schon einmal
ohne Ableitung angegeben:
Die möglichen Übergänge sind in der Abbildung angegeben
(Balmer a-Linie, n = 3 ↔
n = 2). Die aufgrund der Bewegung der H-Atome verbreiterten Linien (Doppler-Verbreiterung)
können mit Hilfe der Dopplerfreien Spektroskopie aufgelöst werden
und die exakte Vermessung der Linienabstände erlaubt eine detaillierte
Überprüfung der Theorie.
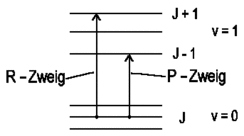
Natürlich muss die Drehimpulserhaltung auch bei Rotationsübergängen
von Molekülen gelten. Für den einfachsten Fall eines linearen
Moleküls, bei dem das (die) Elektron(en) keinen Beitrag zum
Drehimpuls liefern bedeutet der Erhaltungssatz, dass ΔJ
= ±1 ist, d.h. die Rotation kann sich
um 1h erhöhen oder um 1h
erniedrigen, wenn ein Photon absorbiert wird. Man spricht dann vom P-Zweig
(die Rotation wird um 1h erniedrigt) bzw. vom R-Zweig
(die Rotation wird um 1h erhöht).
Wenn der Gesamtdrehimpuls der Elektronen ¹
0 ist, oder wenn das Molekül gewinkelt ist, dann kommt der Vektorcharakter
des Drehimpulses bei den Auswahlregeln zum Tragen, denn nun ist auch ΔJ
= 0 (Q-Zweig) möglich (außer J = 0 →
J = 0 !), da eine Änderung von 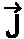 (bzgl. der Richtung) möglich ist, ohne Änderung des Betrages
von J.
(bzgl. der Richtung) möglich ist, ohne Änderung des Betrages
von J.
Bei der Raman-Spektroskopie
sind zwei Photonen involviert: Es findet ein Übergang vom initialen
Zustand i in ein virtuelles Niveau statt und eine "Emission" aus diesem
Zustand in einen finalen Zustand f. Da der Drehimpuls beider Photonen untergebracht
werden muss (Drehimpulserhaltung) folgen daraus die Auswahlregeln für
die Ramanspektroskopie: ΔJ = 0, ±2.
Bei ΔJ = 0 kompensieren sich die Drehimpulse
der beiden Photonen (¯), bei ΔJ
= ±2 addieren sie sich (
bzw.
¯¯). Man erhält so einen S-Zweig (ΔJ
= +2) und einen O-Zweig (ΔJ = -2).

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() verknüpft, das über µ = I · F gegeben
ist. Mit F = π r² (Fläche die überstrichen
wird) erhalten wir µ = I · F = −e/τ
(π r²). Für den Drehimpuls gilt L
= mevr = me2pr²/τ
, da v=2πr/τ
verknüpft, das über µ = I · F gegeben
ist. Mit F = π r² (Fläche die überstrichen
wird) erhalten wir µ = I · F = −e/τ
(π r²). Für den Drehimpuls gilt L
= mevr = me2pr²/τ
, da v=2πr/τ
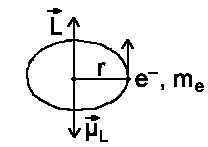 Wir erhalten danach:
Wir erhalten danach:

![]() )
relativ zum Bahndrehimpuls (
)
relativ zum Bahndrehimpuls (![]() )
bewirken eine Verdopplung der Energieniveaus (natürlich außer
s-Niveaus), die spektroskopisch beobachtbar ist, da die Spektrallinie bei
genügend hoher Auflösung als Linienpaar (Dublett) sichtbar wird.
Das bekannteste Beispiel hierfür ist die Natrium D-Linie bei den Wellenlängen
5890 Å und 5896 Å. Zum Verständnis der Spin-Bahn-Kopplung
(oder Wechselwirkung) "setzen" wir uns in Gedanken zunächst auf den
Atomkern: Das Elektron "umkreist" uns (resp. den Kern) mit dem Bahndrehimpuls
)
bewirken eine Verdopplung der Energieniveaus (natürlich außer
s-Niveaus), die spektroskopisch beobachtbar ist, da die Spektrallinie bei
genügend hoher Auflösung als Linienpaar (Dublett) sichtbar wird.
Das bekannteste Beispiel hierfür ist die Natrium D-Linie bei den Wellenlängen
5890 Å und 5896 Å. Zum Verständnis der Spin-Bahn-Kopplung
(oder Wechselwirkung) "setzen" wir uns in Gedanken zunächst auf den
Atomkern: Das Elektron "umkreist" uns (resp. den Kern) mit dem Bahndrehimpuls![]() .
Setzen wir uns auf das Elektron, dann umkreist uns der Kern und erzeugt
ein magnetisches Feld
.
Setzen wir uns auf das Elektron, dann umkreist uns der Kern und erzeugt
ein magnetisches Feld ![]() ,
das parallel zu
,
das parallel zu![]() steht (wegen
der positive Ladung des Kerns). Da das Elektron (auf dem wir in Gedanken
sitzen) ruht, gibt es nun eine Wechselwirkung des magnetischen Feldes mit
dem magnetischen Moment
steht (wegen
der positive Ladung des Kerns). Da das Elektron (auf dem wir in Gedanken
sitzen) ruht, gibt es nun eine Wechselwirkung des magnetischen Feldes mit
dem magnetischen Moment ![]() S
des Spins. Die Wechselwirkung ist proportional zu
S
des Spins. Die Wechselwirkung ist proportional zu ![]() S.
S.![]() .
Da
.
Da ![]() ||
||![]() und
und ![]() S ||
S ||![]() ist die Wechselwirkung proportional zu
ist die Wechselwirkung proportional zu ![]() .
.![]() ,
was den Namen Spin-Bahn-Kopplung erklärt. Die Energie des Elektrons
aufgrund dieser Wechselwirkung ist dann
,
was den Namen Spin-Bahn-Kopplung erklärt. Die Energie des Elektrons
aufgrund dieser Wechselwirkung ist dann
![]() .
.![]() ? Nun, wir
haben als Messgröße (oder Observable) den Gesamtdrehimpuls
? Nun, wir
haben als Messgröße (oder Observable) den Gesamtdrehimpuls ![]() :
:


![]() P
= −gI e
P
= −gI e![]() /
/![]() /
/![]() und
und ![]() koppeln, woraus der
"neue" Gesamtdrehimpuls entsteht:
koppeln, woraus der
"neue" Gesamtdrehimpuls entsteht:
![]() und Auflösen nach
und Auflösen nach ![]() .
.![]() liefert analog
zum Ausdruck für die Feinstruktur die Erwartungswerte für die
Hyperfeinenergie:
liefert analog
zum Ausdruck für die Feinstruktur die Erwartungswerte für die
Hyperfeinenergie:
![]() i
bzw.
i
bzw.![]() f muss
aufgrund der Drehimpulserhaltung gelten:
f muss
aufgrund der Drehimpulserhaltung gelten:


![]() (bzgl. der Richtung) möglich ist, ohne Änderung des Betrages
von J.
(bzgl. der Richtung) möglich ist, ohne Änderung des Betrages
von J.
