Fine, Hyperfine and the Kinetic Moment of Photons

Zeeman Effect

We will consider the influence of a positively charged nucleus on the movement of an electron. In the classical model,the electron (Bohr atom model) is moving along a closed path.  The current arising from this motion is as follows I = −e/τ  (τ: orbital period). The magnetic moment e/τ (π r²). And for the kinetic moment L = mevr = me2pr²/τ  where v=2πr/τ
 

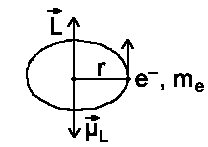Next we obtain:
 

L  =  − e/2me

Since the kinetic moment is represented by an operator in quantum mechanics, we obtain the eigenvalues µLz of z-component   (Lz y = ml h y):

µLz  =  − e/2meh· ml     where     µB  = eh/2me (Bohr Magneton)

 

µLz  =  −µB· ml      where  µB  = eh/2me

µB  =  eh/2me  =  9,273 · 10-24 J/K  =  5,656 . 10-5 eV/T  =  1,4 · 1010 Hz/T         (T: Tesla)

The energy of such a system in the magnetic field is as follows:
 

EB  =  −µLz· B  =  µB · ml· B

and the total energy is E = E0 + EB , i.e. the energy levels having a kinetic moment with quantum number l are split into 2l + 1 new levels:
 
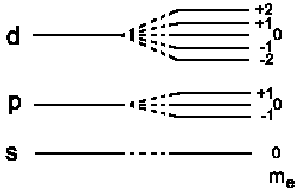This effect is also referred to as ordinary  Zeeman Effect

The hydrogen ground state (ml = 0) stays uninfluenced. This is not accidental because H is a paramagnetic element! The reason so is because of electron spin. Now we consider the spin in classical mechanics as rotating around the axis electron. We also find here
 

µSz  =  −gS µB · ms
EB  =   gS· µB· ms· B

 

The so-called gyromagnetic factor gS is obtained from the relativist Dirac-equation with gS = 2. Experiments give:

gS  =  2,00231930438(6)

This value can be explained by quantum electrodynamics which is the full quantum theory of electromagnetic field. Moreover, the electromagnetic field is expanded into normal vibrations which are quantized like a harmonic oscillator. Additionally, each normal vibration has its zero energy point hw/2. This means there are fluctuating electromagnetic fields even if there is no influence from external fields. Though the average field is zero, the squared average field isn't equal to 0. This leads to the squared average fluctuations of positions. 

One can find more detailed information about the Zeeman effect here.

The value gS · µB≈ 28 GHz/T shows us which energy state is higher according to electron spin interaction with magnetic field. Since now it's possible to produce magnetic fields with the strength of a few Teslas, we expect to detect transitions in GHz region (microwaves) when applying such fields. That's why Electron-Spin-Resonance (ESR) Spectroscopy is involved with microwaves. When applying NMR method we have a deal with MHz region. We will discuss it in more detail later.

Spin-Orbital Coupling

Two possible orientations of electron spin () relative to orbital moment () give rise to energy level doubling (this is not true for s-levels) which are spectroscopically resolved since the spectral lines are detected as a pair of lines (doublet) when one has enough resolution. The most well-known example is the Na D-line at 5890 Å and 5896 Å wavelengths. To understand the physics of spin-orbital coupling (or interaction) lets take a look at the atomic nucleus: the electron revolves around the nucleus and has an electronic orbital moment . The electron produces a magnetic field that is parallel to (because of the positive nucleus charge). Since the electron in disucussion is at rest, we have only the interaction between the magnetic field and the magnetic moment S of spin. This interaction is proportional to S· . Since  ||  and S ||  the interaction is proportional to · , that explains the spin-orbital coupling.  According to this type of interation, the electron energy is as follows.

ESL  =  cSL·  . /h²

where cSL is the proportionality constant which can be derived from the Dirac equation.

And what about .   ? Now we have the total kinetic moment as observable value:

  =   + 

We can't set a vector randomly in quantum mechanics. BY squaring the above equation, we get:

J²  =  L² + S² + 2  .     ® .   =  ½ (J² − L² − S²)

Since the squared kinetic moment is a conservative quantity we can substitute the quantum mechanical operators with eigenvalues (we will now use the small letter for eigenvalues):

.  º L. S  =  ½ [J(J + 1) − L(L + 1) − S(S + 1)] h²

We now obtain for the energy of spin-orbital coupling:

ESL  =  cSL/2[J(J + 1) − L(L + 1) − S(S + 1)]

The value cSL can be directly observed in the doublet structure of the optical spectra.

For H-atom one can obtain (J = L ± S, S = ½)

ESL (­ ≡ J = L + ½)  =  ½ cSL · L

ESL (¯ ≡ J = L − ½)  =  − ½ cSL (L + 1)


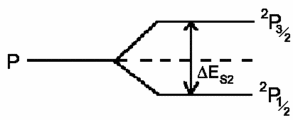J  =  L + S  ≡  1 + ½ = 3/2
J  =  L − S  ≡  1 − ½ = ½

The separation between two levels is as follows

ΔESL  =  ESL(­) − ESL (¯)  =  ½ cSL (2L + 1)


Together with proportionality constant cSL Dirac obtained the energy separation corresponding to spin-orbital interaction:

ΔESL  =  |En| Z²α²/n l(l +1)  ≈  5,3 · 10-5 Z²/n l(l + 1) |En|

where α = e²/4πh²ε0c = 1/137,0359895 is the Sommerfeld fine structure constant. 

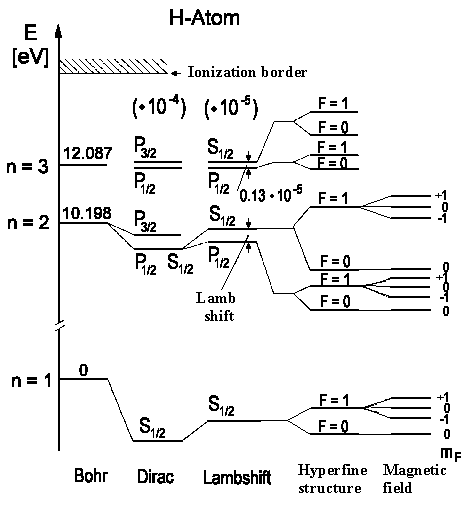
The energy eigenvalues (spin-orbital + relativistic effects) for H-atom are obtained  from the full Dirac theory:

EnJ  =  − mc²/2α²Z²/n²{1 + α²Z²/n(1/J + ½− ¾ n)}

According to this theory, energy levels having the same J and n values are degenerate. For instance, states 2²S½ and 2²P½ would have the same energy. Lamb and Rutherfordproved in 1947 that this degeneracy doesn't correspond to what is observed experimentally. They excited the transition ²S½ ← ²P½ using radiospectroscopy i.e. the energy levels are split and are not degenerate. Moreover this splitting is only about 0,03528 cm-1.


However it's not all concerning level splitting: there is one more spectral line splitting, the so-called hyperfine structure. It's caused by interaction between magnetic field (from electron movement) and nuclear spin. For instance, the hydrogen atom has one proton with spin I = ½ and corresponding magnetic moment P  =  −gI eh/2mp/h = µK/h

Since a proton is heavier than an electron, its magneton µK (µK = gI eh/2mp) is lighter by a factor  me/mp  !

Similar to fine structure coupling, we must connect and  now having "new" total kinetic moment:

  =  + 

where Fy = F(F +1) h² y  and Fzy  =  mF hy   ;     mF = −F, −F+1, ... F−1, F

Squaring the equation for and solving it relatively  .  one can obtain the hyperfine energy structure:

EHFS  =  cHFS/2{F(F + 1) - J(J + 1) - I(I + 1)}

The lowest term of hydrogen 1²S½ is then split into two terms with F = 1 (spin electron and spin proton ­­) and F = 0 (spin electron and spin proton ­¯ antiparallel). The transition between these two levels can only occur when the spin turns over. This, however, is a very rare phenomenon (it, on average, happens once every 10 million years in a hydrogen atom) which is not observable in our Universe. It lies near n» 1,4204 GHz (λ = 21 cm).

Since this transition changes the system kinetic moment from F = 1h into F = 0h but from the fact that the total kinetic moment should be the same follows photon must take the hydrogen atom kinetic moment. And so a photon also possesses kinetic moment.

However, the photon spin is as follows
 

SPhoton = 1h

The photon spin isn't a good designation because the "photon spin" projection on the flight axis can take values m  = +1 or m = -1 for right- and lefthand circular polarized light, correspondingly. And it can never be m=0, that would correspond to the longitudial polarization which is never realized! 

The proton spin has interesting consequences for optical spectra since we obtain the selection rule for transitions. We will have for the final total kinetic moment f of the system that was originally at some initial state i  according to the kinetic moment conservation law: 

i  = f + Photon

Certainly Photon shouldn't be necessarily equal to   because photon can also possess (together with spin) the orbital moment relative to an atom. The photon emission with unchanged orbital moment visually means that photon has left the boundary areas. Nevertheless, this process is very improbable so that quantum numbers Ji and Jf have the following relation according to the kinetic moment conservation law: 
 

ΔJ  =  Jf − Ji  =  0 , ±1

 
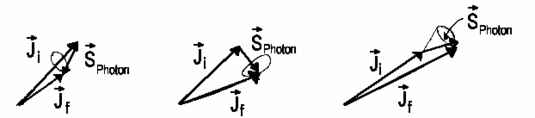ΔJ  =  −1 
ΔM  =  0 , ±1 
P-Branch		 ΔJ  =  0 
ΔM  =  ±1 
Q-Branch		 ΔJ  =  +1 
ΔM  =  0 , ±1 
R-Branch

If  Jf = 0 and Ji = 0 then ΔJ=0 is forbidden according to the kinetic moment conservation law. If there is small interaction between and  then there is special selection rule for spin that states:
 

ΔS  =  0

The selection rule for electron orbital moment has been given here without any derivation:
 

Δl  =  ±1

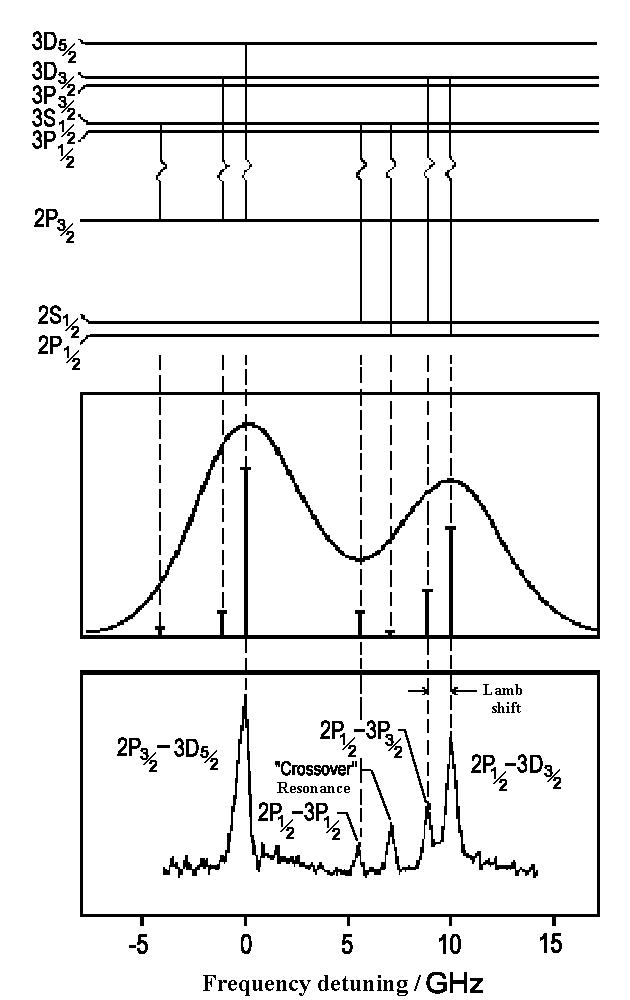
The possible transitions are shown on the illustration to the left (Balmer a-Line, n = 3 ↔  n = 2). Since H atoms move there are Doppler distribution of these optical lines, that can be resolved by using Doppler free spectroscopy which can help us to prove the theory.  

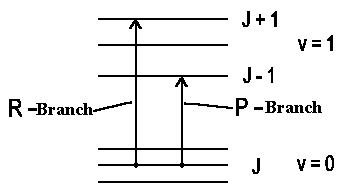
Certainly we must also have kinetic moment conservation for increasing rotation of a molecule. In the simplest case of a linear molecule for which      electron contribution into kinetic moment is small so that ΔJ = ±1, i.e. the rotation can be increased by 1h or decreased by 1h when photon is absorbed. It's said about P-Branch (the rotation is decreased by 1h) and R-Branch (the rotation is increased by 1h).

If total electron kinetic moment isn't equal to 0 or if we have a deal with a non-linear molecule then the kinetic impulse vector character according to the selection rule undergoes some changes, i.e. there is also a transition   DJ = 0 (Q-Branch) possible (when J = 0 → J = 0 !).



In Raman-Spectroscopy two photons are used: the molecule undergoes a transition from the initial state i into virtual state and then there is "emission" from this virtual state into the final state f. Since the kinetic moment of both photons should compensate or add up to each other (the kinetic moment conservation law) it follows the selection rules for the Raman spectroscopy: ΔJ = 0, ±2. When ΔJ = 0 the kinetic moments of both photons compensate each other (­¯); and when ΔJ = ±2 they are added to each other (­­ or ¯¯). One can talk about S-Branch       (ΔJ = +2) and O-Branch (ΔJ = -2) in this case.

Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.