


Next: MCSCF
Up: Das Hartree-Fock-Verfahren
Previous: Einteilchenbasen
Offenschaliges Hartree-Fock
Eine einzelne Slater-Determinante [siehe Gln. (43)] ist im allgemeinen
keine Eigenfunktion zum Spin-Operator 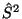 ,
obgleich der
(nicht-relativistische) Hamilton-Operator, Gln. (2), mit
,
obgleich der
(nicht-relativistische) Hamilton-Operator, Gln. (2), mit 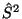 kommutiert (vergleiche Abschnitt 4.4).
Dieses, im Abschnitt 2.2.3 beschriebene, sogenannte
unrestricted Hartree-Fock (UHF) kann daher bei offenschaligen Systemen
Artefakte hervorrufen, die dadurch entstehen, daß sich Zustände mit
verschiedener Symmetrie vermischen.
kommutiert (vergleiche Abschnitt 4.4).
Dieses, im Abschnitt 2.2.3 beschriebene, sogenannte
unrestricted Hartree-Fock (UHF) kann daher bei offenschaligen Systemen
Artefakte hervorrufen, die dadurch entstehen, daß sich Zustände mit
verschiedener Symmetrie vermischen.
Dieses Problem vermeidet man beim sogenannten restricted Hartree-Fock
(RHF) dadurch, daß man symmetrie- und spinadaptierte Linearkombinationen
[sogenannte ``Konfigurationszustandsfunktionen,''
engl. ``Configuration state functions'' (CSF)]
aus verschiedenen, energetisch entarteten Slater-Determinanten, mit paarweise
orthogonalen Spin-Orbitalen, 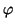 ,
bildet
,
bildet
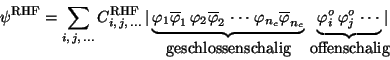 |
(78) |
wobei die Vektorkopplungskoeffizienten
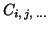 ,
auch
Clebsch-Gordan-Koeffizienten genannt, durch den gewünschten
Zustand exakt festgelegt sind und nicht variiert werden.
Summiert wird über alle (entarteten) Orbitale der jeweiligen offenen
Schale; Orbitale mit
,
auch
Clebsch-Gordan-Koeffizienten genannt, durch den gewünschten
Zustand exakt festgelegt sind und nicht variiert werden.
Summiert wird über alle (entarteten) Orbitale der jeweiligen offenen
Schale; Orbitale mit
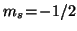 (
(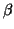 -Spin) werden von solchen mit
-Spin) werden von solchen mit
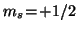 (
(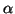 -Spin) durch einen Überstrich unterschieden.
-Spin) durch einen Überstrich unterschieden.
In bestimmten Fällen kann man nach Roothaan [14] den
Energieerwartungswert der RHF-Wellenfunktion (78) schreiben als
(vergleiche Abschnitt 2.2.4)
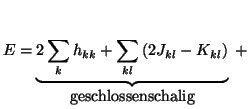 |
| |
|
![$\displaystyle \; +\; f \bigg[
\underbrace{2 \sum_m h_{mm}}_{\mbox{offenschalig}...
...sum_{km} \left( 2 J_{km} - K_{km} \right)
}_{\mbox{WW.\ offen.-geschl.}}
\bigg]$](img164.gif) |
(79) |
Die a, b und f sind numerische Konstanten, die vom jeweiligen Fall
abhängen, z.B. F-Atom: 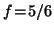 ,
,
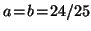 .
.



Next: MCSCF
Up: Das Hartree-Fock-Verfahren
Previous: Einteilchenbasen
Robert Gdanitz
1999-07-05
Auf diesem Webangebot gilt die Datenschutzerklärung der TU Braunschweig mit Ausnahme der Abschnitte VI, VII und VIII.
![]() ,
bildet
,
bildet